
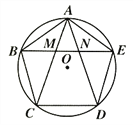
【题目】如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AMAD;③MN=3-![]() ;④S△EBC=2
;④S△EBC=2![]() -1,其中正确的结论是_________(把你认为正确结论的序号都填上).
-1,其中正确的结论是_________(把你认为正确结论的序号都填上).
【答案】①②③
【解析】解:∵∠BAE=∠AED=108°.∵AB=AE=DE,∴∠ABE=∠AEB=∠EAD=36°,∴∠AME=180°﹣∠EAM﹣∠AEM=108°,故①正确;
∵∠AEN=108°﹣36°=72°,∠ANE=36°+36°=72°,∴∠AEN=∠ANE,∴AE=AN,同理DE=DM,∴AE=DM.∵∠EAD=∠AEM=∠ADE=36°,∴△AEM∽△ADE
∴![]() =
=![]() ,∴AE2=AMAD;
,∴AE2=AMAD;
∴AN2=AMAD;故②正确;
∵AE2=AMAD,∴22=(2﹣MN)(4﹣MN),解得:MN=3﹣![]() ;故③正确;
;故③正确;
在正五边形ABCDE中,∵BE=CE=AD=1+![]() ,∴BH=
,∴BH=![]() BC=1,∴EH=
BC=1,∴EH=![]() =
=![]() ,∴S△EBC=
,∴S△EBC=![]() BCEH=
BCEH=![]() ×2×
×2×![]() =
=![]() ,故④错误;
,故④错误;
故答案为:①②③.


科目:初中数学 来源: 题型:
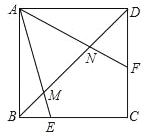
【题目】如图,正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,若DN=1,BM=2,那么MN=_____.证明:DN2+BM2=MN2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:(1)正整数和负整数统称为整数;(2)把能够写成分数形式![]() (m、n是整数,n≠0)的数叫做有理数;(3)异号两数相加,当绝对值不等时,取绝对值较大加数的符号,并用较大的加数减去较小的加数;(4)0是整数,但不是整式.正确的个数有 ( )
(m、n是整数,n≠0)的数叫做有理数;(3)异号两数相加,当绝对值不等时,取绝对值较大加数的符号,并用较大的加数减去较小的加数;(4)0是整数,但不是整式.正确的个数有 ( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
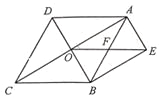
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
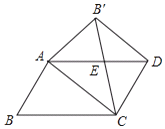
(发现与证明)ABCD中,AB≠BC,将△ABC沿AC翻折至△AB`C,连结B`D.
结论1:△AB`C与ABCD重叠部分的图形是等腰三角形;结论2:B`D∥AC;
(1)请证明结论1和结论2;
(应用与探究)
(2)在ABCD中,已知BC=2,∠B=45°,将△ABC沿AC翻折至△AB`C,连接B`D![]() 若以A、C、D、B`为顶点的四边形是正方形,求AC的长(要求画出图形)
若以A、C、D、B`为顶点的四边形是正方形,求AC的长(要求画出图形)
查看答案和解析>>
科目:初中数学 来源: 题型:
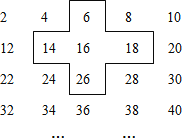
【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在日历中移动的规律后,突发奇想,将连续的得数2,4,6,8,…,排成如图形式:并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)请你选择十字框中你喜欢的任意位置的一个数,将其设为x,并用含x的代数式表示十字框中五个数的和.
(2)若将十字框上下左右移动,可框住另外的五个数,试间:十字框能否框住和等于2015的五个数,如能,请求出这五个数;如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
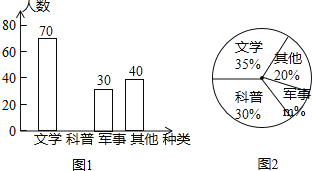
【题目】某学校在开展“书香校园”活动期间,对学生课外阅读的喜好进行抽样调查(每人只选一种书籍),将调查结果绘制成如图所示的两幅不完整的统计图,根据图中的信息,解答下列问题:
(1)这次调查的学生人数为 人,扇形统计图中m的值为 ;
(2)补全条形统计图;
(3)如果这所学校要添置学生课外阅读的书籍1500册,请你估计“科普”类书籍应添置多少册比较合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少?
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com