
【题目】若抛物线的顶点坐标是![]() ,并且抛物线与
,并且抛物线与![]() 轴两交点间的距离为8,试求该抛物线的关系式,并求出这条抛物线上纵坐标为10的点的坐标。
轴两交点间的距离为8,试求该抛物线的关系式,并求出这条抛物线上纵坐标为10的点的坐标。
【答案】![]() ;
;![]() ,
,![]()
【解析】
已知了抛物线的对称轴方程和抛物线与x轴两交点间的距离,可求出抛物线与x轴两交点的坐标;然后用待定系数法求出抛物线的解析式,进而可求出抛物线上纵坐标为10的点的坐标.
解:设该抛物线的关系式为y=a(x-1)2+16,与x轴的两个交点的横坐标为x1,x2,且x1<x2
∴对称轴x=![]() =1,且x2-x1=8;
=1,且x2-x1=8;
解得:x1=-3,x2=5,
∴抛物线与x轴两交点为(-3,0),(5,0);
把点(5,0)代入y=a(x-1)2+16,得:16a+16=0,
∴a=-1;
∴该抛物线的关系式为y=-(x-1)2+16,
即y=-x2+2x+15;
将y=10代入,得:-x2+2x+15=10;
解得x1=![]() ,x2=
,x2=![]() ;
;
∴这条抛物线上纵坐标为10的点的坐标为![]() ,
,![]()


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
查看答案和解析>>
科目:初中数学 来源: 题型:
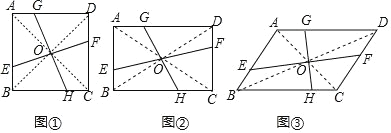
【题目】在四边形 ABCD 中,对角线 AC、BD 相交于点 O,过点 O 的两条直线分别交边 AB、CD、AD、BC 于点 E、F、G、H.
(感知)如图①,若四边形 ABCD 是正方形,且 AG=BE=CH=DF,则 S 四边形AEOG= S 正方形 ABCD;
(拓展)如图②,若四边形 ABCD 是矩形,且 S 四边形 AEOG=![]() S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
(探究)如图③,若四边形 ABCD 是平行四边形,且 AB=3,AD=5,BE=1, 试确定 F、G、H 的位置,使直线 EF、GH 把四边形 ABCD 的面积四等分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.
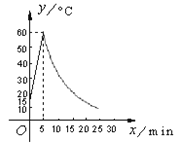
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论:①a﹣b+c<0;②2a+b+c>0;③x(αx+b)≤a+b;④a>﹣1.其中正确的有( )
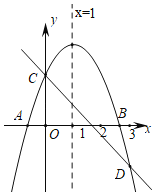
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=
与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=![]() .
.
(1)求抛物线的解析式;
(2)平移直线l经过原点O,得到直线m,点P是直线m上任意一点,PB⊥x轴于点B,PC⊥y轴于点C,若点E在线段OB上,点F在线段OC的延长线上,连接PE,PF,且PE=3PF.求证:PE⊥PF;
(3)若(2)中的点P坐标为(6,2),点E是x轴上的点,点F是y轴上的点,当PE⊥PF时,抛物线上是否存在点Q,使四边形PEQF是矩形?如果存在,请求出点Q的坐标,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】剪纸是中国传统的民间艺术,它画面精美,风格独特,深受大家喜爱,现有三张不透明的卡片,其中两张卡片的正面图案为“金鱼”,另外一张卡片的正面图案为“蝴蝶”,卡片除正面剪纸图案不同外,其余均相同.将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求抽出的两张卡片上的图案都是“金鱼”的概率.(图案为“金鱼”的两张卡片分别记为A1、A2,图案为“蝴蝶”的卡片记为B)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 和反比例函数
和反比例函数![]() .
.
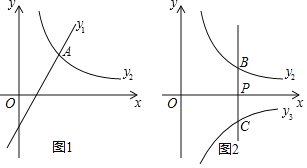
(1)如图1,若![]() ,且函数
,且函数![]() 、
、![]() 的图象都经过点
的图象都经过点![]() .
.
①求![]() ,
,![]() 的值;
的值;
②直接写出当![]() 时
时![]() 的范围;
的范围;
(2)如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 与函数
与函数![]() 的图象相交于点
的图象相交于点![]() ,与反比例函数
,与反比例函数![]() 的图象相交于点
的图象相交于点![]() .
.
①若![]() ,直线
,直线![]() 与函数
与函数![]() 的图象相交点
的图象相交点![]() .当点
.当点![]() 、
、![]() 、
、![]() 中的一点到另外两点的距离相等时,求
中的一点到另外两点的距离相等时,求![]() 的值;
的值;
②过点![]() 作
作![]() 轴的平行线与函数
轴的平行线与函数![]() 的图象相交于点
的图象相交于点![]() .当
.当![]() 的值取不大于1的任意实数时,点
的值取不大于1的任意实数时,点![]() 、
、![]() 间的距离与点
间的距离与点![]() 、
、![]() 间的距离之和
间的距离之和![]() 始终是一个定值.求此时
始终是一个定值.求此时![]() 的值及定值
的值及定值![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com