
 如图,在△ABC中,BC边的中垂线交BC于D,交AB于E,CE平分∠ACB,如果△ABC的周长为20,BD=4,∠B=36°.
如图,在△ABC中,BC边的中垂线交BC于D,交AB于E,CE平分∠ACB,如果△ABC的周长为20,BD=4,∠B=36°.分析 (1)根据线段垂直平分线性质得出BE=CE,BC=2BD=8,求出AB+AC=12,即可求出答案;
(2)求出∠ECB的度数和∠ACB的度数,根据三角形内角和定理求出即可.
解答 解:(1)∵BC边的中垂线交BC于D,交AB于E,BD=4,
∴BE=CE,BC=2BD=8,
∵△ABC的周长为20,
∴AB+AC=20-8=12,
∴△ACE的周长为AE+CE+AC=AE+BE+AC=AB+AC=12;
(2)∵BE=CE,∠B=36°,
∴∠ECB=∠B=36°,
∵CE平分∠ACB,
∴∠ACB=2∠ECB=72°,
∴∠A=180°-∠B-∠ACB=72°.
点评 本题考查的是线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等),难度一般.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
 如图所示,有一个圆柱,它的高为9厘米,底面周长为24厘米,在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物,问它爬行的最短路程是多少厘米?
如图所示,有一个圆柱,它的高为9厘米,底面周长为24厘米,在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物,问它爬行的最短路程是多少厘米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
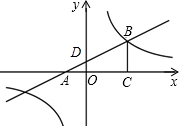 如图,平面直角坐标系中,直线y=$\frac{1}{2}$x+$\frac{1}{2}$与x轴交于点A,与y轴交于点D,与双曲线y=$\frac{k}{x}$在第一象限内交于点B,BC⊥x轴于点C,AB=3AD.求双曲线的解析式.
如图,平面直角坐标系中,直线y=$\frac{1}{2}$x+$\frac{1}{2}$与x轴交于点A,与y轴交于点D,与双曲线y=$\frac{k}{x}$在第一象限内交于点B,BC⊥x轴于点C,AB=3AD.求双曲线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是3,5,2,3,则最大的正方形E的面积为多少?
如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是3,5,2,3,则最大的正方形E的面积为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com