
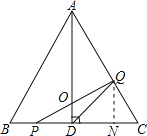
����Ŀ����ͼ���ڡ�ABC�У���֪AB��BC��CA��4cm��AD��BC��D����P��Q�ֱ��B��C����ͬʱ���������е�P��BC���յ�C�˶����ٶ�Ϊ1cm/s����Q��CA��AB���յ�B�˶����ٶ�Ϊ2cm/s���������˶���ʱ��Ϊx(s)��
(1)��xΪ��ֵʱ��PQ��AC��
(2)���PQD�����Ϊ![]() ����0��x��2ʱ����y��x�ĺ�����ϵʽ��
����0��x��2ʱ����y��x�ĺ�����ϵʽ��
(3)��0��x��2ʱ����֤��ADƽ�֡�PQD�������
(4)̽����PQΪֱ����Բ��AC��λ�ù�ϵ����д����Ӧλ�ù�ϵ��x��ȡֵ��Χ(��Ҫ��д������)��

���𰸡���1��![]() ����2��y��
����2��y��![]() ����3�������������4����
����3�������������4����![]() ��
��![]() ��
��![]() ��x��4ʱ����PQΪֱ����Բ��AC�ཻ��
��x��4ʱ����PQΪֱ����Բ��AC�ཻ��
�������������������1����ʹPQ��AC�������·��=�ٶȡ�ʱ���ʾ��CP��CQ�ij����ٸ���30�ȵ�ֱ�������ε������з�����⣻��2����0��x��2ʱ��P��BD�ϣ�Q��AC�ϣ�����Q��QN��BC��N����x��ʾ��PD��QN�ij������������ε������ʽ�������y��x�ĺ�����ϵʽ����3�����������ε������ʽ��Ҫ֤��ADƽ�֡�PQD�������ֻ��֤��O��PQ���е㣮�����������֤��BP=CN����PD=DN���ٸ���ƽ���ߵȷ��߶ζ�������֤������4�����������֪������x��ֵ��ʹ����PQΪֱ����Բ��AC���룬�ɣ�1����֪��x��![]() ʱ����PQΪֱ����Բ��AC���У�����Q��AB��ʱ��8��2x��
ʱ����PQΪֱ����Բ��AC���У�����Q��AB��ʱ��8��2x��![]() �����x��
�����x��![]() ����x��
����x��![]() ��
��![]() ʱ����PQΪֱ����Բ��AC���У�����ֱ����Բ�ཻ��������֪��
ʱ����PQΪֱ����Բ��AC���У�����ֱ����Բ�ཻ��������֪��![]() ��
��![]() ��
��![]() ��x��4ʱ����PQΪֱ����Բ��AC�ཻ��
��x��4ʱ����PQΪֱ����Բ��AC�ཻ��
���������
(1)��Q��AB��ʱ����ȻPQ����ֱ��AC��
��Q��AC��ʱ��������ã�BP��x��CQ��2x��PC��4��x��
��AB��BC��CA��4�����C��60�㣻
��PQ��AC�����С�QPC��30�㣬
��PC��2CQ����4��x��2��2x��
��x��![]() ��
��
(2)��ͼ����0��x��2ʱ��P��BD�ϣ�Q��AC�ϣ�����Q��QN��BC��N��
�ߡ�C��60�㣬QC��2x��
��QN��![]() QC��
QC��![]() x��
x��
��AB��AC��AD��BC��
��BD��CD��![]() BC��2��
BC��2��
��DP��2��x��
��y��![]() PD�qQN��
PD�qQN��![]() x��
x��![]() ��
��
(3)��0��x��2ʱ����Rt��QNC�У�QC��2x����C��60�㣬NC��x��
��BP��NC��
��BD��CD��
��DP��DN��
��AD��BC��QN��BC��
��AD��QN��
��OP��OQ��
��![]() ��
��
��ADƽ�֡�PQD�������
(4)��Ȼ��������x��ֵ��ʹ����PQΪֱ����Բ��AC���룬
��(1)��֪����x��![]() ʱ����PQΪֱ����Բ��AC���У�����Q��AB��ʱ��8��2x��
ʱ����PQΪֱ����Բ��AC���У�����Q��AB��ʱ��8��2x��![]() �����x��
�����x��![]() ��
��
�ʵ�x��![]() ��
��![]() ʱ����PQΪֱ����Բ��AC���У�
ʱ����PQΪֱ����Բ��AC���У�
��![]() ��
��![]() ��
��![]() ��x��4ʱ����PQΪֱ����Բ��AC�ཻ��
��x��4ʱ����PQΪֱ����Բ��AC�ཻ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������,������ȥʱ,����2.1��,�Ժ�ÿ�곤0.3��,��n��������Ϊ________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��-3��4��������ƽ��3����λ��������ƽ��2����λ��õ���Q�����Q��������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
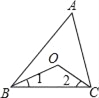
����Ŀ����1����ͼ������ABC�У���ABC����ACB��ƽ�����ཻ�ڵ�O������A=42�㣬����BOC�Ķ�����
��2���ѣ�1������A=42���������ȥ������̽����BOC����A֮����������������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C����O��ֱ��AB�ӳ����ϵ�һ�㣬����BO=BD=BC��
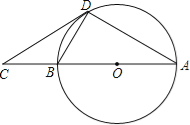
��1����֤��CD����O�����ߣ�
��2�����뾶OB=2����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ���ı��� ABCD������AB��AD�ij��ǹ���x�ķ���![]() ��0������ʵ������
��0������ʵ������
(1)��mΪ��ֵʱ���ı���ABCD�����Σ������ʱ���εı߳���
(2)��AB�ij�Ϊ2����ôƽ���ı���ABCD���ܳ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ��27���������� �� �����P��4����5���͵�Q��a��b������ԭ��Գƣ���a��ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��AD=2��AB=2![]() ���Ե�AΪԲ�ģ�ADΪ�뾶��Բ��BC�����ڵ�E����AB�ڵ�F
���Ե�AΪԲ�ģ�ADΪ�뾶��Բ��BC�����ڵ�E����AB�ڵ�F
��1�����ABE�Ķ�����
��2�����������AFEDΧ��һ��Բ�IJ��棬����Բ�ĵ���뾶�Ƕ�����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com