
分析 (1)根据已知4个等式可得;
(2)根据已知等式得出答案;
(3)利用所得等式的规律列出算式,然后两两相消,计算化简后的算式即可得;
(4)根据已知等式规律,列项相消求解可得.
解答 解:(1)由题意知,a6=$\frac{{2}^{6}}{1+3×{2}^{6}+2×({2}^{6})^{2}}$=$\frac{1}{{2}^{6}+1}$-$\frac{1}{{2}^{7}+1}$,
故答案为:$\frac{{2}^{6}}{1+3×{2}^{6}+2×({2}^{6})^{2}}$,$\frac{1}{{2}^{6}+1}$-$\frac{1}{{2}^{7}+1}$;
(2)an=$\frac{{2}^{n}}{1+3×{2}^{n}+2×({2}^{n})^{2}}$=$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$,
故答案为:$\frac{{2}^{n}}{1+3×{2}^{n}+2×({2}^{n})^{2}}$,$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$;
(3)原式=$\frac{1}{2+1}$-$\frac{1}{{2}^{2}+1}$+$\frac{1}{{2}^{2}+1}$-$\frac{1}{{2}^{3}+1}$+$\frac{1}{{2}^{3}+1}$-$\frac{1}{{2}^{4}+1}$+$\frac{1}{{2}^{4}+1}$-$\frac{1}{{2}^{5}+1}$+$\frac{1}{{2}^{5}+1}$-$\frac{1}{{2}^{6}+1}$+$\frac{1}{{2}^{6}+1}$-$\frac{1}{{2}^{7}+1}$
=$\frac{1}{2+1}$-$\frac{1}{{2}^{7}+1}$
=$\frac{14}{43}$,
故答案为:$\frac{14}{43}$;
(4)原式=$\frac{1}{2+1}$-$\frac{1}{{2}^{2}+1}$+$\frac{1}{{2}^{2}+1}$-$\frac{1}{{2}^{3}+1}$+…+$\frac{1}{{2}^{n}+1}$-$\frac{1}{{2}^{n+1}+1}$
=$\frac{1}{2+1}$-$\frac{1}{{2}^{n+1}+1}$
=$\frac{{2}^{n+1}-2}{3({2}^{n+1}+1)}$.
点评 本题主要考查数字的变化,解题的关键是根据已知等式得出等式的变化规律及列项相消法求解.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
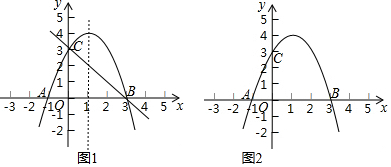
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
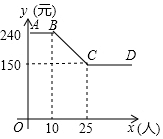 某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
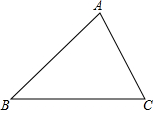 如图,已知△ABC中,AB=4,AC=3.
如图,已知△ABC中,AB=4,AC=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com