
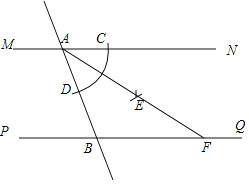
【题目】如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用以下步骤作图:
①以点A为圆心,适当长为半径作弧交射线AN于点C,交线段AB于点D;
②以点C为圆心,适当长为半径画弧;然后再以点D为圆心,同样长为半径画弧.前后两弧在∠NAB内交于点E;
③作射线AE,交PQ于点F;
若AF=2![]() ,∠FAN=30°,则线段BF的长为_____.
,∠FAN=30°,则线段BF的长为_____.
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为![]() 万元/辆,经销一段时间后发现:当该型号汽车售价定为
万元/辆,经销一段时间后发现:当该型号汽车售价定为![]() 万元/辆时,平均每周售出
万元/辆时,平均每周售出![]() 辆;售价每降低
辆;售价每降低![]() 万元,平均每周多售出
万元,平均每周多售出![]() 辆.
辆.
(1)当售价为![]() 万元/辆时,平均每周的销售利润为___________万元;
万元/辆时,平均每周的销售利润为___________万元;
(2)若该店计划平均每周的销售利润是![]() 万元,为了尽快减少库存,求每辆汽车的售价.
万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
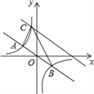
【题目】如图,在直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线y=﹣![]() x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,DE平分∠ADB交AB于点E,过点C作CF∥AB交ED延长线于点F,若∠A=48°.
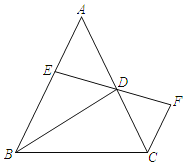
(1)求∠DBC的度数;
(2)求∠F的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
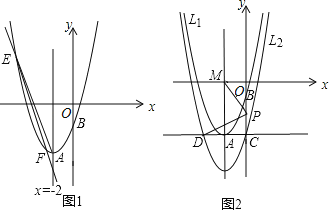
【题目】抛物线l1:y=x2+bx+c与它的对称轴x=﹣2交于点A,且经过点B(0,﹣2).
(1)求抛物线l1的解析式;
(2)如图1,直线y=kx+2k﹣8(k<0)与抛物线l1交于点E,F,若△AEF的面积为![]() ,求k的值;
,求k的值;
(3)如图2,将抛物线l1向下平移n(n>0)个单位长度得到抛物线l2,抛物线l2与y轴交于点C,过点C作x轴的平行线交抛物线l2于另一点D;抛物线l2的对称轴与x轴的交于点M,P为线段OC上一点,若△POM与△PCD相似,并且符合该条件的点P有且只有2个,求n的值及相应点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.
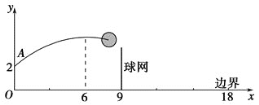
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:

(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com