
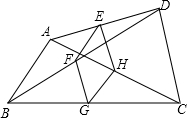
 如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,
如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,分析 (1)首先利用三角形的中位线定理证出EF∥AB,EF=$\frac{1}{2}$AB,HG∥AB,HG=$\frac{1}{2}$AB,可得四边形EFGH是平行四边形;
(2)根据邻边相等的平行四边形是菱形,添加条件AB=CD后,证明EF=EH即可.
解答 解:(1)∵E,F是AD,DB中点,
∴EF∥AB,EF=$\frac{1}{2}$AB,
∵H,G是AC,BC中点,
∴HG∥AB,HG=$\frac{1}{2}$AB,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形,
(2)需添加条件AB=CD.
∵E,H是AD,AC中点,
∴EH=$\frac{1}{2}$CD,
∵AB=CD,
∴EF=EH,
∴四边形EFGH是菱形.
点评 此题主要考查了三角形中位线定理与菱性的判定方法,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:填空题
 如图,已知直线AB:y=kx+2k+2与抛物线y=x2交于点A、B,当∠AOB>90°,则k的取值范围为k<-$\frac{3}{2}$.
如图,已知直线AB:y=kx+2k+2与抛物线y=x2交于点A、B,当∠AOB>90°,则k的取值范围为k<-$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:解答题
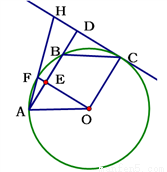
如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D, 延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)求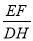 的比值;若DH=6,求EF和半径OA的长.
的比值;若DH=6,求EF和半径OA的长.
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:判断题
在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,当5≤m<10时为B级,当0≤m<5时为C级.现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下:
11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(1)求样本数据中为A级的频率;
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数
(3)从样本数据为C级的人中随机抽取2人,用树状图或列表法求抽得2个人的“日均发微博条数”都是3的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com