
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
【答案】(1)=;(2)=,过程见解析;(3)CD的长是1或3.
【解析】试题分析:(1)根据△ABC是等边三角形,点E为AB的中点,即可得出CE⊥AB,进而得出∠ECB=∠D=∠DEB=30°,即可得出线段AE与DB的大小关系;
(2)首先得出BE=CF,进而得出∠EDB=∠ECB,∠BED=∠FCE,进而利用△DBE≌△EFC即可得出答案;
(3)分两种情况进行讨论,①当E在线段BA的延长线上,D在线段BC的延长线上;②当E在线段AB的延长线上,D在线段CB的延长线上.
试题解析:(1)∵△ABC是等边三角形,点E为AB的中点,
∴∠ABC=60°,CE⊥AB,
∴AE=BE,
∴∠ECB=∠D=∠DEB=30°,
∴AE=DB,
故答案为:=;
(2) 在等边△ABC中,
∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠AFE=60°=∠BAC,
∴AE=AF=EF,
∴AB-AE=AC-AF,
即BE=CF,
∵∠ABC=∠EDB+∠BED=60°,
∠ACB=∠ECB+∠FCE=60°,
∵ED=EC,
∴∠EDB=∠ECB,
∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∴∠BED=∠FCE,
∴△DBE≌△EFC(SAS)
∴DB=EF,
∴AE=BD,
故答案为:=;
(3)CD的长是1或3.
参考做法如下:
当E在线段BA的延长线上,D在线段BC的延长线上时,如图1所示,
过E作EF⊥BD,垂足为F点,可得∠EFB=90°,
∵EC=ED,∴F为CD的中点,即CF=DF=![]() CD,
CD,
∵△ABC为等边三角形,∴∠ABC=60°,
∴∠BEF=30°,
∵BE=AB+AE=1+2=3,
∴FB=![]() EB=
EB=![]() ,
,
∴CF=FB-BC=![]() ,
,
则CD=2CF=1;
当E在线段AB的延长线上,D在线段CB的延长线上时,如图2所示,
过E作EF⊥BD,垂足为F点,可得∠EFC=90°,
∵EC=ED,∴F为CD的中点,即CF=DF=![]() CD,
CD,
∵△ABC为等边三角形,∴∠ABC=∠EBF=60°,
∴∠BEF=30°,
∵BE=AE-AB=2-1=1,
∴FB=![]() BE=
BE=![]() ,
,
∴CF=BC+FB=![]() ,
,
则CD=2CF=3,
综上,CD的值为1或3.
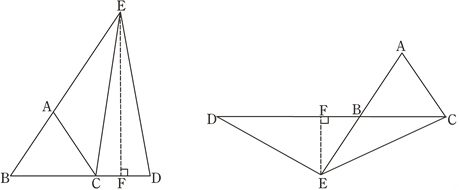
图1 图2


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是( )

A.2B.4C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出一种情形):_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在△ABC中,已知∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.请写出图中的等腰三角形,并找出EF与BE、CF间的关系;
(2) 如图②中∠ABC的平分线与三角形ABC的外角∠ACG的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.图中有等腰三角形吗?如果有,请写出来.EF与BE、CF间的关系如何?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=![]() ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平整的桌面上,有若干个棱长为![]() 的小正方体堆成一个几何体,如图所示
的小正方体堆成一个几何体,如图所示

(1)分别画出这个几何体从上面、左面看到的图形;
(2)如果把露在外面的面都涂上颜色,求涂上颜色的面的面积;
(3)若你手里还有一些相同的小正方体,如果保持从上面、左面看到的图形不变,最多可以再添加几个小正方体?直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条长1200 m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0),交y轴于点C,点D是线段OB上一动点,连接CD,将CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF,CE交于点G.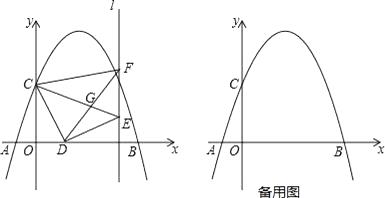
(1)求抛物线解析式;
(2)求线段DF的长;
(3)当DG= ![]() 时,
时,
①求tan∠CGD的值;
②试探究在x轴上方的抛物线上,是否存在点P,使∠EDP=45°?若存在,请写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com