
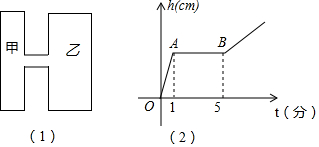
| A. | 5cm | B. | 4cm | C. | 3cm | D. | 2cm |
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:选择题
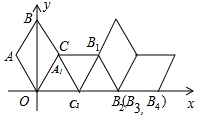 如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1,A2,A3,…,则A2015的坐标为.( )
如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1,A2,A3,…,则A2015的坐标为.( )| A. | (1343,0) | B. | (1347,0) | C. | (1343$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | D. | (1347$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>1 | B. | m<$\frac{1}{2}$ | C. | $\frac{1}{2}$<m<1 | D. | m<$\frac{1}{2}$或m>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
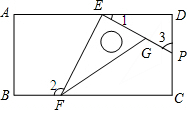 如图,一个含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠3=65°,那么∠2的度数是( )
如图,一个含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠3=65°,那么∠2的度数是( )| A. | 100° | B. | 105° | C. | 115° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
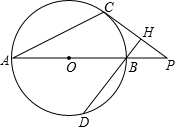 如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC.
如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (m-2)(m+2)=m2-2 | B. | (x-6)(x+6)=x2+36 | C. | (x-y)(x+y)=x2-y2 | D. | (x+y)(x+y)=x2+y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com