Question

16．在A型纸片（边长为a的正方形），B型纸片（边长为b的正方形），C型纸片（长为a，宽为b的长方形）各
若干张．
（1）取A型纸片1张，B型纸片4张，C型纸片4张，拼成一个大正方形，画出示意图，你能得到反映整式乘法运算过程的等式吗？
（2）分别取A型、B型、C型纸片若干张，拼成一个正方形，使所拼正方形的面积为4a²+4ab+b²，画出示意图，你能得到反映因式分解过程的等式吗？
（3）用这3种纸片，每种各10张，从其中取出若干张卡片，每种至少取1张，把取出的纸片拼成一个正方形，请问一共能拼出多少种不同大小的正方形？简述理由．

Answer 1

分析 （1）如图所示，根据边长和面积写出等式即可；
（2）如图所示，根据面积的等式画出图形，并根据边长分解因式；
（3）有六种不同大小的正方形．

解答 解：（1）如图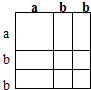

得：（a+2b）（a+2b）=a²+4ab+4b²；
（2）如图，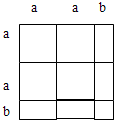

得：4a²+4ab+b²=（2a+b）²；
（3）（a+b）²=a²+2ab+b²
（a+2b）²=a²+4ab+4b²
（a+3b）²=a²+6ab+9b²
（2a+b）²=4a²+4ab+b²
（2a+2b）²=4a²+8ab+4b²
（3a+b）²=9a²+6ab+b²
（3a+2b）²=9a²+12ab+4b²（不合题意）
所以可以拼出6种不同大小的正方形．

点评 本题考查了因式分解的意义和完全平方公式的几何背景，与几何图形相结合，利用组合后所成长方形的面积与组合图形的面积相等列式即可．