
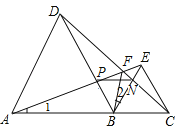
【题目】如图,点A,B,C在一条直线上,△ABD,△BC均为等边三角形,连接AE、CD,PN、BF下列结论:①△ABE≌△DBC;②∠DFA=60°;③△BPN为等边三角形;④若∠1=∠2,则FB平分∠AFC.其中结论正确的有( )
A. 4个B. 3个C. 2个D. 1个
【答案】A
【解析】
由等边三角形的性质得出AB=DB,∠ABD=∠CBE=60°,BE=BC,得出∠ABE=∠DBC,由SAS即可证出△ABE≌△DBC;由△ABE≌△DBC,得出∠BAE=∠BDC,根据三角形外角的性质得出∠DFA=60°;由ASA证明△ABP≌△DBN,得出对应边相等BP=BN,即可得出△BPN为等边三角形;证明P、B、N、F四点共圆,由圆周角定理得出∠BFP=∠BFN,即FB平分∠AFC.
∵△ABD、△BCE为等边三角形,
∴AB=DB,∠ABD=∠CBE=60°,BE=BC,
∴∠ABE=∠DBC,∠PBN=60°,
在△ABE和△DBC中,
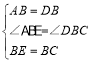 ,
,
∴△ABE≌△DBC(SAS),
∴①正确;
∵△ABE≌△DBC,
∴∠BAE=∠BDC,
∵∠BDC+∠BCD=180°﹣60°﹣60°=60°,
∴∠DFA=∠BAE+∠BCD=∠BDC+∠BCD=60°,
∴②正确;
在△ABP和△DBN中,
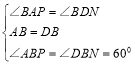 ,
,
∴△ABP≌△DBN(ASA),
∴BP=BN,
∴△BPN为等边三角形,
∴③正确;
∵∠DFA=60°,
∴∠AFC=120°,
∴∠AFC+∠PBN=180°,
∴P、B、N、F四点共圆,
∵BP=BN,
∴弧BP=弧BN,
∴∠BFP=∠BFN,
即FB平分∠AFC;
∴④正确;
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() (a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(a≠0)与y轴交与点C(0,3),与x轴交于A、B两点,点B坐标为(4,0),抛物线的对称轴方程为x=1.
(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点N从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,设△MBN的面积为S,点M运动时间为t,试求S与t的函数关系,并求S的最大值;
(3)在点M运动过程中,是否存在某一时刻t,使△MBN为直角三角形?若存在,求出t值;若不存在,请说明理由.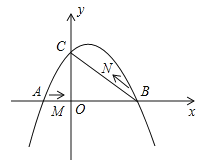
查看答案和解析>>
科目:初中数学 来源: 题型:
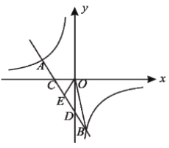
【题目】双曲线![]() (k为常数,且
(k为常数,且![]() )与直线
)与直线![]() 交于
交于![]() 两点.
两点.
(1)求k与b的值;
(2)如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,点A(﹣2,2)和点B(﹣3,﹣2)的位置如图所示.
(1)作出线段AB关于y轴对称的线段A′B′,并写出点A、B的对称点A′、B′的坐标;
(2)连接AA′和BB′,请在图中画一条线段,将图中的四边形AA′B′B分成两个图形,其中一个是轴对称图形,另一个是中心对称图形,并且线段的一个端点为四边形的顶点,另一个端点在四边形一边的格点上.(每个小正方形的顶点均为格点).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在布袋中装有两个大小一样,质地相同的球,其中一个为红色,一个为白色、模拟“摸出一个球是白球”的机会,可以用下列哪种替代物进行实验( )
A. “抛掷一枚普通骰子出现1点朝上”的机会
B. “抛掷一枚啤酒瓶盖出现盖面朝上”的机会
C. “抛掷一枚质地均匀的硬币出现正面朝上”的机会
D. “抛掷一枚普通图钉出现针尖触地”的机会
查看答案和解析>>
科目:初中数学 来源: 题型:
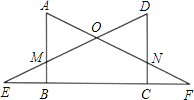
【题目】如图,AB⊥EF,DC⊥EF,垂足分别为B、C,且AB=CD,BE=CF.AF、DE相交于点O,AF、DC相交于点N,DE、AB相交于点M.
(1)请直接写出图中所有的等腰三角形;
(2)求证:△ABF≌△DCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2经过点A(4,0),B(1,0).
(1)求出抛物线的解析式;
(2)点D是直线AC上方的抛物线上的一点,求△DCA面积的最大值;
(3)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理.

查看答案和解析>>
科目:初中数学 来源: 题型:
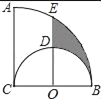
【题目】如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为O.以点C为圆心,BC为半径作弧AB,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )

A. AE=CF B. DE=BF C. ∠ADE=∠CBF D. ∠AED=∠CFB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com