
 如图,已知四边形ABCD中,两组对边延长后分别交于,Q两点,∠P,∠Q的平分线交于M.
如图,已知四边形ABCD中,两组对边延长后分别交于,Q两点,∠P,∠Q的平分线交于M.分析 (1)连接PQ,由三角形的内角和得到∠QCP=180°-∠1-∠2,由角平分线的定义得到∠AQB=2∠3,∠APD=2∠4,根据三角形的内角和即可得到结论;
(2)由(1)知,∠QMP=$\frac{1}{2}$(∠BCD+∠A)
根据已知条件即可得到结论.
解答 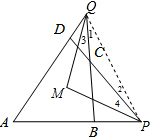 解:(1)连接PQ,
解:(1)连接PQ,
∵∠QCP=180°-∠1-∠2,
∠A=180°-∠AQP-∠APQ=180°-∠1-∠2-∠AQB-∠APD
又∵∠P,∠Q的平分线交于M,
∴∠AQB=2∠3,∠APD=2∠4,
∴∠QCP+∠A=(180°-∠1-∠2)+(180°-∠1-∠2-2∠3-2∠4)
=360°-2∠1-2∠2-2∠3-2∠4,
∴$\frac{1}{2}$(∠QCP+∠A)=180°-∠1-∠2-∠3-∠4,
又∵∠BCD=∠QCP,
∴$\frac{1}{2}$(∠BCD+∠A)=180°-∠1-∠2-∠3-∠4,
又∵∠QMP=180°-∠MQP-∠MPQ=180°-∠1-∠3-∠2-∠4,
∴∠QMP=$\frac{1}{2}$(∠BCD+∠A)=$\frac{1}{2}$×(150°+60°)=105°;
(2)由(1)知,∠QMP=$\frac{1}{2}$(∠BCD+∠A)
∵∠A+∠QCP=180°,
∴∠A+∠BCD=180°,
∴∠QMP=90°,
∴PM⊥QM.
点评 本题考查的是三角形内角和定理,角平分线的定义,熟知三角形内角和是180°是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 在公园调查了1000名老年人的健康状况 | |
| B. | 利用派出所的户籍网随机调查了该地区10%的老年人健康状况 | |
| C. | 调查了10名老年邻居的健康状况 | |
| D. | 在医院调查了1000名老年人的健康状况 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com