
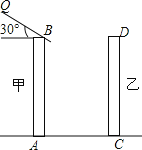
【题目】如图,是住宅区内的两幢楼,它们的高![]() ,两楼间的距离
,两楼间的距离![]() ,现需了解甲楼对乙楼的采光的影响情况.
,现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为![]() 角时,求甲楼的影子在乙楼上有多高(答案可用根号表示);
角时,求甲楼的影子在乙楼上有多高(答案可用根号表示);
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一轮船以30km/h的速度由西向东航行,在途中接到台风警报,台风中心正以20km/h的速度由南向北移动.已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.
问:(1)如果轮船不改变航向,轮船会不会进入台风影响区?
(2)若轮船进入台风影响区,那么从接到警报开始,经多少时间就进入台风影响区?(结果精确到0.01h)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A(-1,3),B(3,
的图象交于A(-1,3),B(3,![]() )两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.

(1)求一次函数及反比例函数的解析式;
(2)若点P在直线![]() 上,且S△ACP=2S△BDP,求点P的坐标.
上,且S△ACP=2S△BDP,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知定义
在一次数学活动课中,老师给出这样一个新定义:如果三角形的两个内角α与β满足α+2β=90°,那么我们称这样的三角形为“类直角三角形”.
尝试运用
(1)如图1,在Rt△ABC中,∠C=90°,BC=3,AB=5,BD是∠ABC的平分线.
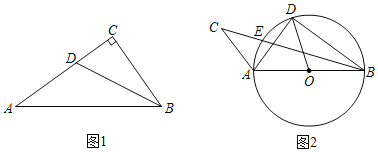
①证明△ABD是“类直角三角形”;
②试问在边AC上是否存在点E(异于点D),使得△ABE也是“类直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
类比拓展
(2)如图2,△ABD内接于⊙O,直径AB=10,弦AD=6,点E是弧AD上一动点(包括端点A,D),延长BE至点C,连结AC,且∠CAD=∠AOD,当△ABC是“类直角三角形”时,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com