
【题目】如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点在同一条直线上,连接BD,则下列结论错误的是( )
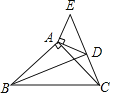
A. △ABD≌△ACE B. ∠ACE+∠DBC=45°
C. BD⊥CE D. ∠BAE+∠CAD=200°
【答案】D
【解析】
根据SAS即可证明△ABD≌△ACE,再利用全等三角形的性质以及等腰直角三角形的性质即可一一判断.
∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
在△BAD和△CAE中,∵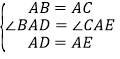 ,∴△BAD≌△CAE(SAS),∴BD=CE,故A正确;
,∴△BAD≌△CAE(SAS),∴BD=CE,故A正确;
∵△ABC为等腰直角三角形,∴∠ABC=∠ACB=45°,∴∠ABD+∠DBC=45°.
∵△BAD≌△CAE,∴∠ABD=∠ACE,∴∠ACE+∠DBC=45°,故B正确.
∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°,∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,则BD⊥CE,故C正确.
∵∠BAC=∠DAE=90°,∴∠BAE+∠DAC=360°﹣90°﹣90°=180°,故D错误.
故选D.


科目:初中数学 来源: 题型:
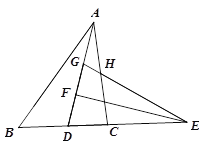
【题目】如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
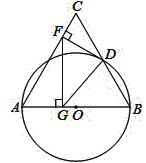
【题目】如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
(1)求证:DF是⊙O的切线;
(2)若AB=12,求FG的长;
(3)在(2)问条件下,求点D到FG的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
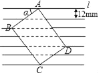
【题目】如图,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上.已知α=36°,求长方形卡片的周长.
(精确到1mm,参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张矩形纸片ABCD,![]() ,
,![]() .
.
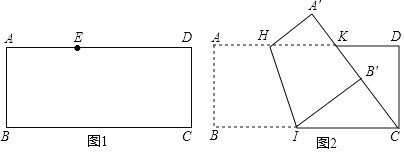
![]() 如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为
如图1,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为![]() 点M,N分别在边AD,BC上
点M,N分别在边AD,BC上![]() ,利用直尺和圆规画出折痕
,利用直尺和圆规画出折痕![]() 不写作法,保留作图痕迹
不写作法,保留作图痕迹![]() ;
;
![]() 如图2,点K在这张矩形纸片的边AD上,
如图2,点K在这张矩形纸片的边AD上,![]() ,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点
,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点![]() ,
,![]() 处,小明认为
处,小明认为![]() 所在直线恰好经过点D,他的判断是否正确,请说明理由.
所在直线恰好经过点D,他的判断是否正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年东京奥运会的比赛门票开始接受公众预订.下表为奥运会官方票务网站公布的几种球类比赛的门票的人民币价格,球迷小李用12000元做为预订下表中比赛项目门票的资金.
比赛项目 | 票价(元/场) |
男篮 | 1000 |
足球 | 800 |
乒乓球 | 500 |
(1)若全部资金用来预订男篮门票和乒乓球门票共15张,问男篮门票和乒乓球门票各订多少张?
(2)若在准备资金允许的范围内和总票数不变的前提下,这个球迷想预定上表中三种球类门票,其中足球门票与乒乓球门票数相同,且足球门票的费用不超过男篮门票的费用,问可以预订这三种球类门票各多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
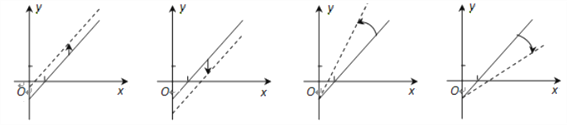
④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com