
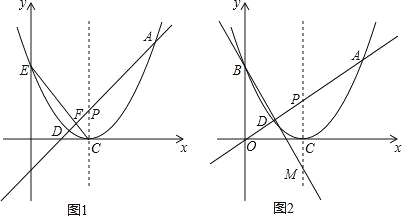
【题目】如图,在平面直角坐标系xOy中,抛物线y=![]() x2-3x+
x2-3x+![]() 交y轴于点E,C为抛物线的顶点,直线AD:y=kx+b(k>0)与抛物线相交于A,D两点(点D在点A的下方).
交y轴于点E,C为抛物线的顶点,直线AD:y=kx+b(k>0)与抛物线相交于A,D两点(点D在点A的下方).
(1)当k=2,b=-3![]() 时,求A,D两点坐标;
时,求A,D两点坐标;
(2)当b=2-3k时,直线AD交抛物线的对称轴于点P,交线段CE于点F,求![]() 的最小值;
的最小值;
(3)当b=0时,若B是抛物线上点A的对称点,直线BD交对称轴于点M,求证:PC=CM.
【答案】(1)A(8,![]() ),D(2,
),D(2,![]() ).(2)
).(2)![]() 的最小值为
的最小值为![]() .(3)证明见解析.
.(3)证明见解析.
【解析】
试题分析:(1)将两函数解析式联立即可组成方程组,解方程组即可;
(2)设D(t,![]() t2-3t+
t2-3t+![]() ),N(t,-
),N(t,-![]() t+
t+![]() ),得出ND=-
),得出ND=-![]() t2+
t2+![]() t=-
t=-![]() (t-
(t-![]() )2+
)2+![]() ,即可求出最大值;
,即可求出最大值;
(3)设点A、D的坐标分别为A(x1,y1)、D(x2,y2),设P、M的坐标分别为P(3,n),M(3,m),连接AB交PC于点H,过点D作DG∥x轴交PC于点G,如图2,则DG∥AB∥x轴,得到方程②③④,将②、③、④代入①中,得m=-3k即可.
试题解析:(1)当k=2,b=-3![]() 时,直线方程化为y=2x-3
时,直线方程化为y=2x-3![]() ,
,
联立两方程可得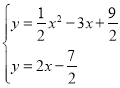 ,
,
解得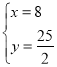 ,
,![]() ;
;
可知,A(8,![]() ),D(2,
),D(2,![]() ).
).
(2)∵y=![]() (x-3)2,
(x-3)2,
∴点P的横坐标为3,
当x=3,b=2-3k时,y=2,
∴点P的坐标为(3,2),
∵CE的解析式为y=-![]() x+
x+![]() ,
,
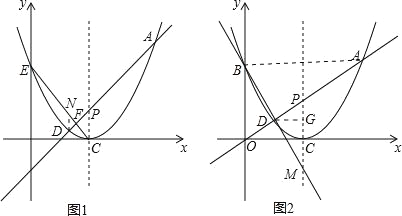
过点D作DN∥PC交CE于点N,如图1,
∴![]() ,
,
设D(t,![]() t2-3t+
t2-3t+![]() ),N(t,-
),N(t,-![]() t+
t+![]() ),
),
∴ND=-![]() t2+
t2+![]() t=-
t=-![]() (t-
(t-![]() )2+
)2+![]() ,
,
当t=![]() 时,ND的最大值为
时,ND的最大值为![]() .
.
∴![]() 的最小值为
的最小值为![]() .
.
(3)设点A、D的坐标分别为A(x1,y1)、D(x2,y2),设P、M的坐标分别为P(3,n),
M(3,m),
∵点A、D在直线y=kx与抛物线的交点,
∴kx1=![]() x12-3x1+
x12-3x1+![]() ,kx2=
,kx2=![]() x22-3x2+
x22-3x2+![]() ,
,
∴x1、x2是方程![]() x2-3x+
x2-3x+![]() =0的两根.
=0的两根.
∴x1+x2=6+2k,x1x2=9,
连接AB交PC于点H,过点D作DG∥x轴交PC于点G,如图2,
则DG∥AB∥x轴,
∴![]() ,
,![]() ,
,
∵BH=AH,
∴![]() ,
,
即![]() ,
,
∴(y2-m)(y1-n)=(y1-m)(n-y2),
整理得2y1y2+2mn=(y1+y2)(m+n)①,
∵x1+x2=6+2k,x1x2=9,
∴y1y2=k2x1x2=9k2②,y1+y2=6k+2k2③,
∵点P(3,n)在直线y=kx上,
∴n=3k④,
将②、③、④代入①中,得m=-3k,
∵定点C的坐标为(3,0),
∴PC=MC.


科目:初中数学 来源: 题型:
【题目】某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,设每次降价的百分率为x,则下面所列的方程中正确的是( )
A. 560(1﹣x)2=315 B. 560(1+x)2=315 C. 560(1﹣2x)2=315 D. 560(1﹣x2)=315
查看答案和解析>>
科目:初中数学 来源: 题型:
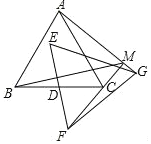
【题目】如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( )
A.2-![]() B.
B.![]() +1 C.
+1 C.![]() D.
D.![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG.
(1)求证:AE=CG;
(2)试判断BE和DF的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(k﹣1)x2+4x+1=0有实数根,则k的取值范围是( )
A. k≤5 B. k<5,且k≠1 C. k≤5,且k≠1 D. k<5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com