
·ÖÎö £¨1£©ÏȼÆËãСÀ¨ºÅÄÚµÄʽ×Ó£¬È»ºó¸ù¾ÝÓÐÀíÊýµÄ³Ë³ý·¨½øÐмÆËã¼´¿É½â´ð±¾Ì⣻
£¨2£©¸ù¾ÝÓÐÀíÊýµÄ³Ë³ý·¨ºÍ¼õ·¨¿ÉÒÔ½â´ð±¾Ì⣻
£¨3£©¸ù¾ÝÓÐÀíÊýµÄ³Ë³ý·¨ºÍ¼õ·¨¿ÉÒÔ½â´ð±¾Ì⣻
£¨4£©ÏȼÆËãСÀ¨ºÅÄÚµÄʽ×Ó£¬È»ºó¸ù¾ÝÓÐÀíÊýµÄ³Ë³ý·¨½øÐмÆËã¼´¿É½â´ð±¾Ì⣻
£¨5£©¸ù¾ÝÓÐÀíÊýµÄ³Ë³ý·¨ºÍ¼Ó¼õ·¨¿ÉÒÔ½â´ð±¾Ì⣻
£¨6£©ÏȼÆËãСÀ¨ºÅÄÚµÄʽ×Ó£¬È»ºó¸ù¾ÝÓÐÀíÊýµÄ³ý·¨¿ÉÒÔ½â´ð±¾Ì⣮
½â´ð ½â£º£¨1£©-3.5¡Á£¨-$\frac{1}{6}$-0.5£©¡Á$\frac{3}{7}$¡Â£¨-$\frac{1}{2}$£©
=-3.5¡Á£¨-$\frac{2}{3}$£©¡Á$\frac{3}{7}¡Á£¨-2£©$
=-2£»
£¨2£©23¡Á£¨-5£©-£¨-3£©¡Â£¨$\frac{3}{128}$£©
=£¨-115£©+3¡Á$\frac{128}{3}$
=£¨-115£©+128
=13£»
£¨3£©|-$\frac{3}{4}$|¡Â£¨-3$\frac{3}{4}$£©-$\frac{9}{14}$¡Á£¨-3$\frac{1}{2}$£©
=$\frac{3}{4}¡Á£¨-\frac{4}{15}£©+\frac{9}{14}¡Á\frac{7}{2}$
=$-\frac{1}{5}+\frac{9}{4}$
=$-\frac{41}{20}$£»
£¨4£©2$\frac{3}{7}$¡Á£¨2$\frac{5}{8}$-4$\frac{5}{8}$£©¡Á$\frac{7}{17}$¡Â1$\frac{1}{17}$
=$\frac{17}{7}¡Á£¨-2£©¡Á\frac{7}{17}¡Á\frac{17}{18}$
=-$\frac{17}{9}$£»
£¨5£©$\frac{7}{12}$¡Â£¨-$\frac{1}{5}$£©+£¨-20£©¡Â$\frac{12}{7}$-$\frac{7}{12}$¡Â£¨-$\frac{1}{13}$£©
=$\frac{7}{12}¡Á£¨-5£©+£¨-20£©¡Á\frac{7}{12}+\frac{7}{12}¡Á13$
=$\frac{7}{12}$¡Á[£¨-5£©+£¨-20£©+13]
=$\frac{7}{12}¡Á£¨-12£©$
=-7£»
£¨6£©-$\frac{1}{60}$¡Â£¨-$\frac{1}{6}$-$\frac{3}{20}$+$\frac{4}{5}$-$\frac{11}{12}$£©
=$-\frac{1}{60}¡Â\frac{-10-9+48-55}{60}$
=$-\frac{1}{60}¡Â\frac{-26}{60}$
=$\frac{1}{60}¡Á\frac{60}{26}$
=$\frac{1}{26}$£®
µãÆÀ ±¾Ì⿼²éÓÐÀíÊýµÄ»ìºÏÔËË㣬½âÌâµÄ¹Ø¼üÊÇÃ÷È·ÓÐÀíÊý»ìºÏÔËËãµÄ¼ÆËã·½·¨£®



| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | 9 | B£® | ¡À9 | C£® | $\sqrt{3}$ | D£® | $¡À\sqrt{3}$ |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
 Èçͼ£¬¡÷ABCÓë¡÷ADE¶¼ÊǵÈÑüÈý½ÇÐΣ¬AD=AE£¬AB=AC£¬¡ÏDAB=¡ÏCAE£¬ÇóÖ¤£º¡÷ABC¡×¡÷ADE£®
Èçͼ£¬¡÷ABCÓë¡÷ADE¶¼ÊǵÈÑüÈý½ÇÐΣ¬AD=AE£¬AB=AC£¬¡ÏDAB=¡ÏCAE£¬ÇóÖ¤£º¡÷ABC¡×¡÷ADE£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º2016-2017ѧÄê¹ã¶«Ê¡·ðɽÊÐ˳µÂÇøÆßÄ꼶3ÔÂÔ¿¼ÊýѧÊÔ¾í£¨½âÎö°æ£© ÌâÐÍ£ºµ¥Ñ¡Ìâ
ÏÂÁÐʽ×Ó²»ÄÜÓÃƽ·½²î¹«Ê½¼ÆËãµÄÊÇ£º£¨ £©
A.  B.
B. 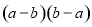
C.  D.
D. 
²é¿´´ð°¸ºÍ½âÎö>>
°Ù¶ÈÖÂÐÅ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com