
 个单位的速度沿DA向点A匀速运动;设点P、Q运动时间为t(秒)
个单位的速度沿DA向点A匀速运动;设点P、Q运动时间为t(秒) ?
?
 ,解关于t的方程,得到满足条件的t的值即可.
,解关于t的方程,得到满足条件的t的值即可. =5,
=5, =5
=5 ,
, =3
=3 ;
;
 t,CQ=3
t,CQ=3 -
- t,
t, ,
, t,AH=
t,AH= t,
t, QC•PH=
QC•PH= •(3
•(3 -
- t)•
t)• t=-2t2+6t(0<t≤2.5)
t=-2t2+6t(0<t≤2.5)
 ,
, -
- t,CH=2
t,CH=2 -
- t,
t, PH•CQ=
PH•CQ= •(4
•(4 -
- t)•(3
t)•(3 -
- t)=2t2-16t+30(2.5<t<3);
t)=2t2-16t+30(2.5<t<3); -
- t,
t,
 PH•CQ=
PH•CQ= •(4
•(4 -
- t)•(
t)•( t-3
t-3 )=-2t2+16t-30(3<t<5);
)=-2t2+16t-30(3<t<5); t,AH=
t,AH= t,
t,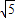 -
- t-
t- t=5
t=5 -
- t,
t, ,
, =
= ,解得t=
,解得t= ;
; -
- t,CH=2
t,CH=2 -
- t,
t, -
- t+2
t+2 -
- t=5
t=5 -
- t,
t, ,
, -
- t):(5
t):(5 -
- t)=
t)= ,解得t=
,解得t= (舍去);
(舍去); -
- t,CH=2
t,CH=2 -
- t,
t, t-3
t-3 -(2
-(2 -
- t)=
t)= t-5
t-5 ,
, ,
, -
- t):(
t):( t-5
t-5 )=
)= ,解得t=
,解得t= ;
; 或
或 时,tan∠PQH=
时,tan∠PQH= .
.

科目:初中数学 来源: 题型:
| 5 |
 A向点A匀速运动;设点P、Q运动时间为t(秒)
A向点A匀速运动;设点P、Q运动时间为t(秒)| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=
如图,菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 个单位的速度沿D
个单位的速度沿D A向点A匀速运动;设点P、Q运动时间为t(秒)
A向点A匀速运动;设点P、Q运动时间为t(秒) ?
?查看答案和解析>>
科目:初中数学 来源:2012-2013学年新人教版九年级(上)期中数学试卷(8)(解析版) 题型:填空题
 ,则点A的坐标为 ;点B的坐标为 .
,则点A的坐标为 ;点B的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com