
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
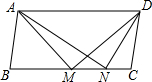 如图,平行四边形ABCD中,M、N是BC边上的点,且∠AMD=∠AND=90°,则下列结论中一定成立的是(1)(3)(4)(把所有正确结论的序号都填在横线上)
如图,平行四边形ABCD中,M、N是BC边上的点,且∠AMD=∠AND=90°,则下列结论中一定成立的是(1)(3)(4)(把所有正确结论的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
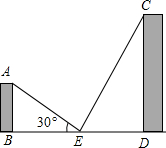 如图,两座建筑物AB与CD,其地面距离BD为60米,E为BD的中点,从E点测得A的仰角为30°,从C处测得E的俯角为60°,现准备在点A与点C之间拉一条绳子挂上小彩旗(不计绳子弯曲),求绳子AC的长度.(结果保留一位小数,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,两座建筑物AB与CD,其地面距离BD为60米,E为BD的中点,从E点测得A的仰角为30°,从C处测得E的俯角为60°,现准备在点A与点C之间拉一条绳子挂上小彩旗(不计绳子弯曲),求绳子AC的长度.(结果保留一位小数,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
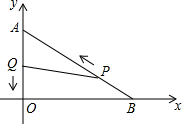 如图,在平面直角坐标系中,已知OA=6厘米,OB=8厘米.点P从点B开始沿BA边向终点A以1厘米/秒的速度移动;点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动.若P、Q同时出发,运动时间为t(s).
如图,在平面直角坐标系中,已知OA=6厘米,OB=8厘米.点P从点B开始沿BA边向终点A以1厘米/秒的速度移动;点Q从点A开始沿AO边向终点O以1厘米/秒的速度移动.若P、Q同时出发,运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
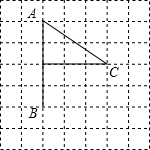 如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )| A. | (2,3) | B. | (1,3) | C. | (3,1) | D. | (3,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com