
【题目】(1)发现规律:
特例1:![]() =
=![]() =
=![]() =
=![]() ;
;
特例2:![]() =
=![]() =
=![]() =
=![]() ;
;
特例3:![]() =4
=4![]() ;
;
特例4:______(填写一个符合上述运算特征的例子);
(2)归纳猜想:
如果n为正整数,用含n的式子表示上述的运算规律为:______;
(3)证明猜想:
(4)应用规律:
①化简:![]() ×
×![]() =______;
=______;
②若![]() =19
=19![]() ,(m,n均为正整数),则m+n的值为______.
,(m,n均为正整数),则m+n的值为______.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析;(4)①2020
;(3)见解析;(4)①2020![]() ;②m+n=38
;②m+n=38
【解析】
(1)根据题目中的例子可以写出例4;
(2)根据(1)中特例,可以写出相应的猜想;
(3)根据(2)中的猜想,对等号左边的式子化简,即可得到等号右边的式子,从而可以解答本题;
(4)①②根据(2)中的规律即可求解.
解:(1)![]() ,
,
故答案为:![]() ;
;
(2)![]() ,
,
故答案为:![]() ;
;
(3)证明:∵左边=![]() ,
,
∵n为正整数,
∴n+1>0.
∴左边=|n+1(n+1)![]() ,
,
又∵右边=(n+1)![]() ,
,
∴左边=右边.
即![]() ;
;
(4)①![]() ×
×![]() =2020
=2020![]() ×
×![]() =2020
=2020![]() ;
;
故答案为:2020![]() ;
;
②∵![]() =19
=19![]() ,
,
∴m+1=19,解得m=18,
∴n=m+2=20,
∴m+n=38.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(﹣5,0)、(﹣2,0).点P在抛物线y=﹣2x2+4x+8上,设点P的横坐标为m.当0≤m≤3时,△PAB的面积S的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
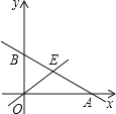
【题目】如图,直线y=-![]() x+b与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
x+b与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3.
(1)求点E的坐标和b的值;
(2)在x轴上有点P(m,0),过点P作x轴的垂线,与直线y=-![]() x+b交于点C,与直线y=x交于点D.若CD≤4,求m的取值范围.
x+b交于点C,与直线y=x交于点D.若CD≤4,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元/吨和100元/吨.经协商,从甲仓库到工厂的运价可优惠a元吨(10≤a≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);
(3)在(2)的条件下,请根据函数的性质说明:随着m的增大,W的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司为“见义勇为基金会”各捐款3000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐20元.请你根据上述信息,就这两个公司的“人数”或“人均捐款”提出一个用分式方程解决的题,并写出解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①HE=HF;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2![]() .以上结论中,你认为正确的有( )个.
.以上结论中,你认为正确的有( )个.
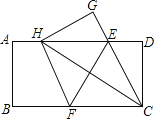
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 y-2 与 x+1 成正比例,当 x=7 时,y=6,
(1)写出 y 与 x 之间的函数关系式;
(2)当 y=-2 时,求 x 的值;
(3)若点 P(-6,m+4)在该函数图象上,求 m 的值
查看答案和解析>>
科目:初中数学 来源: 题型:
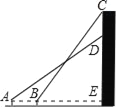
【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(![]() ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清明节假期,小红和小阳随爸妈去旅游,他们在景点看到一棵古松树,小红惊讶的说:“呀!这棵树真高!有60多米.”小阳却不以为然:“60多米?我看没有.”两个人争论不休,爸爸笑着说:“别争了,正好我带了一副三角板,用你们学过的知识量一量、算一算,看谁说的对吧!”
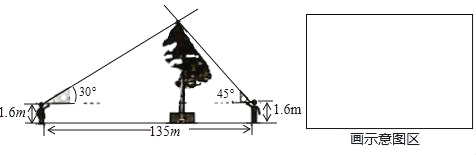
小红和小阳进行了以下测量:如图所示,小红和小阳分别在树的东西两侧同一地平线上,他们用手平托三角板,保持三角板的一条直角边与地平面平行,然后前后移动各自位置,使目光沿着三角板的斜边正好经过树的最高点,这时,测得小红和小阳之间的距离为135米,他们的眼睛到地面的距离都是1.6米.
(1)请在指定区域内画出小红和小阳测量古松树高的示意图;
(2)通过计算说明小红和小阳谁的说法正确(计算结果精确到0.1)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com