
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.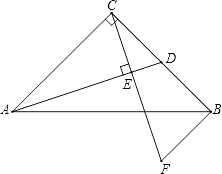
(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
【答案】
(1)解:∵在Rt△ABC中,∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°,
∵CE⊥AD,
∴∠CAD=∠BCF,
∵BF∥AC,
∴∠FBA=∠CAB=45°
∴∠ACB=∠CBF=90°,
在△ACD与△CBF中,
∵ 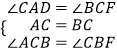 ,
,
∴△ACD≌△CBF;
(2)解:证明:∵∠BCE+∠ACE=90°,∠ACE+∠CAE=90°,
∴∠BCE=∠CAE.
∵AC⊥BC,BF∥AC.
∴BF⊥BC.
∴∠ACD=∠CBF=90°,
在△ACD与△CBF中,
∵ 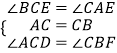 ,
,
∴△ACD≌△CBF,
∴CD=BF.
∵CD=BD= ![]() BC,
BC,
∴BF=BD.
∴△BFD为等腰直角三角形.
∵∠ACB=90°,CA=CB,
∴∠ABC=45°.
∵∠FBD=90°,
∴∠ABF=45°.
∴∠ABC=∠ABF,即BA是∠FBD的平分线.
∴BA是FD边上的高线,BA又是边FD的中线,
即AB垂直平分DF
【解析】(1)根据∠ACB=90°,AC=BC,求得∠CAD=∠BCF,再利用BF∥AC,求得∠ACB=∠CBF=90°,然后利用ASA即可证明△ACD≌△CBF,
(2)利用同角的余角相等得出,∠BCE=∠CAE,再根据平行线的性质得出∠ACD=∠CBF=90°,然后由ASA判定△ACD≌△CBF得到BF=BD,再根据角度之间的数量关系求出∠ABC=∠ABF,即BA是∠FBD的平分线,从而利用等腰三角形三线合一的性质求证即可
【考点精析】根据题目的已知条件,利用平行线的性质和等腰三角形的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】每年淘宝网都会举办“双十一”购物狂欢节,许多商家都会利用这个契机进行打折让利的促销活动.甲网店销售一件A商品的成本为36元,网上标价为110元.“双十一”活动当天,为了吸引买主,连续两次降价销售A商品,问平均每次降价率为多少时,才能使这件A商品的利润率为10%?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某小区的两幢10层住宅楼间的距离为AC="30" m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3 m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α .

(1) 用含α的式子表示h(不必指出α的取值范围);
(2) 当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光 ?
查看答案和解析>>
科目:初中数学 来源: 题型:
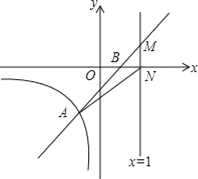
【题目】直线y=kx+b与反比例函数y=![]() (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN=![]() ,求t的值.
,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P位于x轴下方,距离x轴5个单位,位于y轴右方,距离y轴3个单位,那么P点的坐标是( )
A.(5,-3) B.(3,-5) C.(-5,3) D.(-3,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB=![]() ,则GE的长为_____,并简述求GE长的思路.
,则GE的长为_____,并简述求GE长的思路.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com