
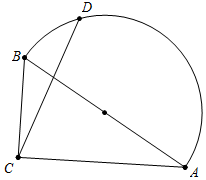
 ��ͼ����Rt��ABC�У���ACB=90�㣬tan��CAB=$\frac{\sqrt{3}}{3}$��AB=3����D����б��ABΪֱ���İ�Բ�ϣ���M��CD�����ȷֵ㣬����D���Ű�Բ���ӵ�A�˶�����Bʱ����M�˶���·����Ϊ��������
��ͼ����Rt��ABC�У���ACB=90�㣬tan��CAB=$\frac{\sqrt{3}}{3}$��AB=3����D����б��ABΪֱ���İ�Բ�ϣ���M��CD�����ȷֵ㣬����D���Ű�Բ���ӵ�A�˶�����Bʱ����M�˶���·����Ϊ��������| A�� | �л�$\frac{��}{2}$ | B�� | $\frac{��}{2}$��$\frac{��}{3}$ | C�� | $\frac{��}{3}$��� | D�� | $\frac{��}{4}$��$\frac{��}{3}$ |
���� ��ͼ����D��B�غ�ʱ������֤����M�Ĺ켣����EFΪֱ���İ�Բ����������֪EF=2���ɵõ�M�˶���·����Ϊ�У���CM��=$\frac{1}{3}$CDʱ��ͬ���ɵõ�M�˶���·������
��� �⣺��ͼ��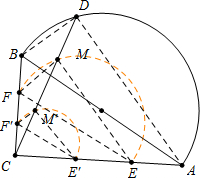
����D��B�غ�ʱ��M��F�غϣ�����D��A�غ�ʱ��M��E�غϣ�����BD��FM��AD��EM��
��$\frac{CF}{BC}$=$\frac{CM}{CD}$=$\frac{CE}{CA}$=$\frac{2}{3}$ʱ����֪FM��BD��EM��AD��
���FMC=��BDC����CME=��CDA��
��AB��ֱ����
���BDA=90�㣬
���FME=��BDA=90�㣬
���M�Ĺ켣����BCΪֱ���İ�Բ����������֪EF=2��
���M�˶���·����Ϊ�У�
��CM��=$\frac{1}{3}$CDʱ��ͬ���ɵõ�M�˶���·����Ϊ$\frac{1}{2}$�У�
��ѡA��
���� ���⿼��켣��ֱ�������ε����ʡ�Բ���й�֪ʶ��ƽ���ߵ��ж������ʵ�֪ʶ������Ĺؼ���ȷ����M���˶��켣�������п�ѡ�����е�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ƽ��ֱ������ϵ�У���֪��A��8��0���͵�B��0��6������C��AB���е㣬��P������AOB�ϣ�ֱ��CP�ء�AOB�����õ����������AOB���ƣ���ô��P�������ǣ�0��3������4��0������$\frac{7}{4}$��0����
��ͼ��ƽ��ֱ������ϵ�У���֪��A��8��0���͵�B��0��6������C��AB���е㣬��P������AOB�ϣ�ֱ��CP�ء�AOB�����õ����������AOB���ƣ���ô��P�������ǣ�0��3������4��0������$\frac{7}{4}$��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
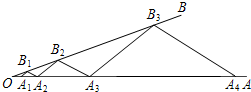 ��ͼ����A1��A2������OA�ϣ�B1������OB�ϣ�������A2B2��A1B1��A3B2��A2B1��A3B3��A2B2��A4B3��A3B2����������A2B1B2�͡�A3B2B3������ֱ�Ϊ1��9�����A1007B1007A1008�������32011��
��ͼ����A1��A2������OA�ϣ�B1������OB�ϣ�������A2B2��A1B1��A3B2��A2B1��A3B3��A2B2��A4B3��A3B2����������A2B1B2�͡�A3B2B3������ֱ�Ϊ1��9�����A1007B1007A1008�������32011���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com