
【题目】如图,□ABCD的对角线AC、BD交于点O,AE平分BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①AE=CE;②S△ABC=ABAC;③S△ABE=2S△AOE;④OE=
BC,连接OE.下列结论:①AE=CE;②S△ABC=ABAC;③S△ABE=2S△AOE;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A.1个B.2个C.3个D.4
【答案】C
【解析】
利用平行四边形的性质可得∠ABC=∠ADC=60°,∠BAD=120°,利用角平分线的性质证明△ABE是等边三角形,然后推出AE=BE=![]() BC,再结合等腰三角形的性质:等边对等角、三线合一进行推理即可.
BC,再结合等腰三角形的性质:等边对等角、三线合一进行推理即可.
∵四边形ABCD是平行四边形,
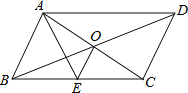
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,∠AEB=60°,
∵AB=![]() BC,
BC,
∴AE=BE=![]() BC,
BC,
∴AE=CE,故①正确;
∴∠EAC=∠ACE=30°
∴∠BAC=90°,
∴S△ABC=![]() ABAC,故②错误;
ABAC,故②错误;
∵BE=EC,
∴E为BC中点,O为AC中点,
∴S△ABE=S△ACE=2 S△AOE,故③正确;
∵四边形ABCD是平行四边形,
∴AC=CO,
∵AE=CE,
∴EO⊥AC,
∵∠ACE=30°,
∴EO=![]() EC,
EC,
∵EC=![]() AB,
AB,
∴OE=![]() BC,故④正确;
BC,故④正确;
故正确的个数为3个,
故选:C.


科目:初中数学 来源: 题型:
【题目】某服装店老板到厂家购甲、乙两种品牌的服装,若购甲种品牌服装10件,乙种品牌服装9件,需要1800元;若购进甲种品牌服装8件,乙种品牌服装18件,需要2520元.
(1)求甲、乙两种品牌的服装每件分别为多少元?
(2)若销售一件甲种品牌服装可获利18元,销售一件乙种品牌服装可获利30元,根据市场需要,服装店老板决定:购进甲种品牌服装的数量要比购进乙种品牌服装的数量的2倍还多4件,且甲种品牌服装最多可购进28件,这样服装全部售出后可使总的获利不少于732元,问有几种进货方案?并写出进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
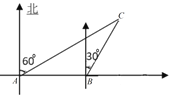
【题目】如图,某货船以24海里/时的速度将一批重要物资从![]() 处运往正东方向的M处,在点
处运往正东方向的M处,在点![]() 处测得某岛
处测得某岛![]() 在北偏东
在北偏东![]() 的方向上.该货船航行
的方向上.该货船航行![]() 分钟后到达
分钟后到达![]() 处,此时再测得该岛在北偏东
处,此时再测得该岛在北偏东![]() 的方向上,已知在
的方向上,已知在![]() 岛周围
岛周围![]() 海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求BP:PQ:QR.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力y随时间t(分钟)的变化规律有如下关系式:  (y值越大表示接受能力越强)
(y值越大表示接受能力越强)
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中;
(2)讲课开始后多少分钟,学生的注意力最集中能持续多少分钟;
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目:初中数学 来源: 题型:
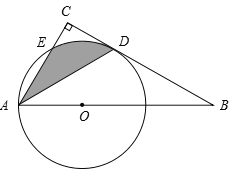
【题目】如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC相切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留π![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l是四边形ABCD的对称轴.若AD∥BC,则下列结论:(1)AB∥CD;(2)AB=BC;(3)BD平分∠ABC;(4)AO=CO.其中正确的有______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
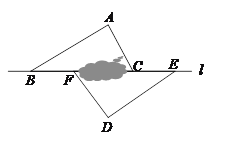
【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OE平分∠BOD,∠AOC=70°,∠DOF=90°.

(1)图中与∠EOF互余的角是 ;
(2)求∠EOF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com