
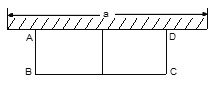
【题目】如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为a为15米),围成中间隔有一道篱笆的长方形花圃。
①如果要围成面积为45平方米的花圃,AB的长是多少米?
②能围成面积比45平方米更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
【答案】(1)AB的长为3m或5m;(2)当AB长为4m,BC为12m时,有最大面积,为48平方米.
【解析】
(1)设AB的长是x米,则BC的长为(24-3x)米,根据矩形的面积公式得到关于x的方程,然后求解方程即可;
(2)利用配方法将(1)中的一元二次方程变形即可得到答案.
(1)设AB的长是x米,则BC的长为(24-3x)米,
根据题意得:(24-3x)x=45,
解得x1=3,x2=5,
当x=3时,长方形花圃的长为24-3x=15;
当x=5时,长方形花圃的长为24-3x=9,
均符合题意;
∴AB的长为3m或5m;
(2)花圃的面积为:(24-3x)x=-3x2+24x=-3(x2-8x+16-16)=-3(x-4)2+48,
∴当AB长为4m,BC为12m时,有最大面积,为48平方米.


科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
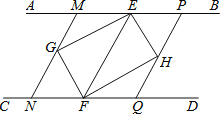
【题目】如图,AB∥CD,点 E、F 分别在 AB、CD 上,连接 EF.∠AEF、∠CF的平分线交于点 G,∠BEF、∠DFE 的平分线交于点 H.求证:四边形 EGFH 是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晨光文具店有一套体育用品:1个篮球,1个排球和1个足球,一套售价300元,也可以单独出售,小攀同学共有50元、20元、10元三种面额钞票各若干张.如果单独出售,每个球只能用到同一种面额的钞票去购买.若小面额的钱的张数恰等于另两种面额钱张数的乘积,那么所有可能中单独购买三个球中所用到的钱最少的一个球是___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
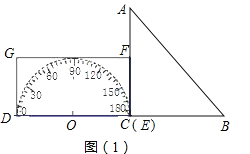
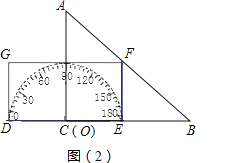
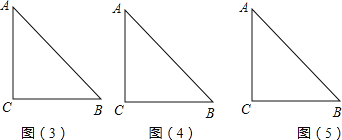
【题目】如图,形如三角板的ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,形如矩形量角器的半圆O的直径DE=12cm,矩形DEFG的宽EF=6cm,矩形量角器以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在BC所在的直线上,设运动时间为x(s),矩形量角器和ABC的重叠部分的面积为S(cm2).当x=0(s)时,点E与点C重合.(图(3)、图(4)、图(5)供操作用).
(1)当x=3时,如图(2),求S, 当x=6时,求S,当x=9时,求S;(直接写结果)
(2)当3<x<6时,求S关于x的函数关系式;
(3)当6<x<9时,求S关于x的函数关系式;
(4)当x为何值时, ABC的斜边所在的直线与半圆O所在的圆相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,∠BAD=∠CDA=90°,AB=![]() ,CD=2
,CD=2![]() ,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2
,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2![]() ;④AE=
;④AE=![]() .其中正确的结论是( )
.其中正确的结论是( )
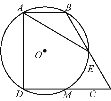
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com