
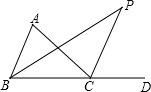
 如图,△ABC一内角和外角角平分线相交于点P,已知∠A的度数为α,则∠BPC的度数是
如图,△ABC一内角和外角角平分线相交于点P,已知∠A的度数为α,则∠BPC的度数是| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 解:∵BP为∠ABC的内角平分线,CP为△ABC外角∠ACD的平分线,两角平分线交于点P,
解:∵BP为∠ABC的内角平分线,CP为△ABC外角∠ACD的平分线,两角平分线交于点P,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
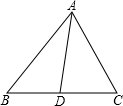
 24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;
24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;查看答案和解析>>
科目:初中数学 来源: 题型:
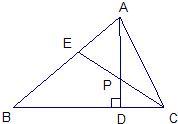 21、如图,△ABC中AD是BC边上的高,CE是△ABC的一条角平分线,它们相交于点P.已知∠APE=55°,∠AEP=75°,求△ABC的各个内角的度数.
21、如图,△ABC中AD是BC边上的高,CE是△ABC的一条角平分线,它们相交于点P.已知∠APE=55°,∠AEP=75°,求△ABC的各个内角的度数.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| BD |
| DC |
| AB |
| AC |
| BD |
| DC |
| AB |
| AC |
| BD |
| DC |
| AB |
| AC |
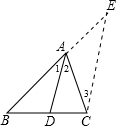 E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
E∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明| BD |
| DC |
| AB |
| AC |
|
|
| BD |
| DC |
| AB |
| AC |
 []
[]查看答案和解析>>
科目:初中数学 来源: 题型:
 学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.| 6 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com