
【题目】如图,已知![]() 的面积是12,
的面积是12,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,在边
上,在边![]() 上依次作了
上依次作了![]() 个全等的小正方形,
个全等的小正方形,![]() ,
,![]() ,
,![]() ,
,![]() ,则每个小正方形的边长为( )
,则每个小正方形的边长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
设正方形的边长为x,根据正方形的性质以及相似三角形性质先求出相应情况下的正方形边长,然后进一步寻求规律即可.

当作了1个正方形时,如图所示,
过A作AM⊥BC,垂足为M,交GH于N,
∴∠AMC=90°,
∵四边形EFGH为正方形,
∴GH∥BC,GH=GF,GF⊥BC,
∴∠AGH=∠B,∠ANH=∠AMC=90°,
∵∠GAH=∠BAC,
∴△AGH~△ABC,
∴AN:AM=GH:BC,
∵△ABC面积为12,BC为6,
∴![]() ,
,
∴AM=4,
设GH=![]() ,
,
∵GF=NM=GH,
∴AN=AMNM=AMGH=![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理,当![]() 时,根据正方形性质可得:DN=2DE,
时,根据正方形性质可得:DN=2DE,
∴![]() ,
,
∴![]() ,
,
以此类推,当为第n个正方形时,每个小正方形边长为:![]() ,
,
故选:D.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() .已知A(-2,0)、B(6,0)、D(0,3)反比例函数
.已知A(-2,0)、B(6,0)、D(0,3)反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求点![]() 的坐标和反比例函数
的坐标和反比例函数![]() 的解析式;
的解析式;
(2)将四边形![]() 沿
沿![]() 轴向上平移
轴向上平移![]() 个单位长度得到四边形
个单位长度得到四边形![]() ,问点
,问点![]() 是否落在(1)中的反比例函数的图象上?
是否落在(1)中的反比例函数的图象上?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
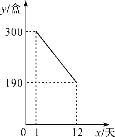
【题目】某公司开发出一款新包装的牛奶,牛奶的成本价为6元/盒,这种新包装的牛奶在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/盒.前几天的销量每况愈下,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的线段表示前12天日销售量y(盒)与销售时间x(天)之间的函数关系,于是从第13天起采用打折销售(不低于成本价),时间每增加1天,日销售量就增加10盒.
(1)打折销售后,第17天的日销售量为________盒;
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)已知日销售利润不低于560元的天数共有6天,设打折销售的折扣为a折,试确定a的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
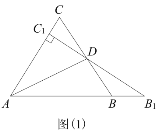
【题目】如图(1)所示,等边△ABC中,线段AD为其内角角平分线,过D点的直线B1C1⊥AC于点C1交AB的延长线于点B1.
(1)请你探究:![]() =
=![]() ,
,![]() =
=![]() 是否都成立?
是否都成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角角平分线,请问![]() =
=![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
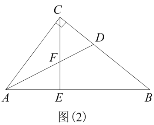
(3)如图(2)所示Rt△ABC中,∠ACB=90°,AC=8,AB=![]() ,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求
,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,运动时间为
匀速运动,运动时间为![]() 秒(
秒(![]() ),连接
),连接![]() 。
。
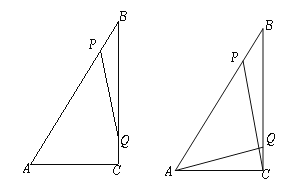
(1)若![]() 与
与![]() 相似,求
相似,求![]() 的值;
的值;
(2)连接![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题.
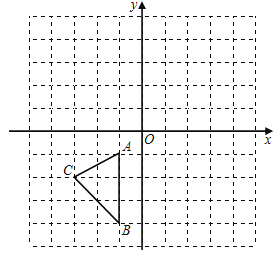
(1)以原点O为对称中心作△ABC的中心对称图形,得到△A1B1C1,请画出△A1B1C1,并直接写出点A1,B1,C1的坐标;
(2)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
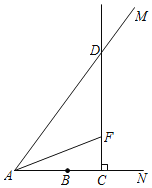
【题目】如图,射线![]() 上有一点
上有一点![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发以每秒3个单位长度的速度沿射线
出发以每秒3个单位长度的速度沿射线![]() 运动,过点
运动,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,在射线
,在射线![]() 上取点
上取点![]() ,使得
,使得![]() ,连结
,连结![]() .设点
.设点![]() 的运动时间是
的运动时间是![]() (秒)(
(秒)(![]() ).
).
(1)当点![]() 在点
在点![]() 右侧时,求
右侧时,求![]() 、
、![]() 的长. (用含
的长. (用含![]() 的代数式表示)
的代数式表示)
(2)连结![]() ,设
,设![]() 的面积为
的面积为![]() 平方单位,求
平方单位,求![]() 与
与![]() 之间的丽数关系式.
之间的丽数关系式.
(3)当![]() 是轴对称图形时,直接写出
是轴对称图形时,直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com