
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线 (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(1)如果b=-2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式。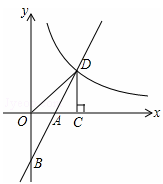
(1)4; (2)y=x.
解析试题分析:(1)首先求出直线y=2x-2与坐标轴交点的坐标,然后由△AOB≌△ACD得到CD=OB,AO=AC,即可求出D坐标,由点D在双曲线y= ( x>0)的图象上求出k的值;
( x>0)的图象上求出k的值;
(2)首先直线y=2x+b与坐标轴交点的坐标为A(-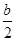 ,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
(1)当b=-2时,
直线y=2x-2与坐标轴交点的坐标为A(1,0),B(0,-2).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(2,2).
∵点D在双曲线y= ( x>0)的图象上,
( x>0)的图象上,
∴k=2×2=4.
(2)直线y=2x+b与坐标轴交点的坐标为A(-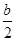 ,0),B(0,b).
,0),B(0,b).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(-b,-b).
∵点D在双曲线y= ( x>0)的图象上,
( x>0)的图象上,
∴k=(-b)•(-b)=b2.
即k与b的数量关系为:k=b2.
直线OD的解析式为:y=x.
考点:反比例函数综合题.


科目:初中数学 来源: 题型:解答题
某校校长暑假带领该市市级“三好学生”去北京旅游.甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内的全部按全票价的6折优惠”(即按全票的60%收费).若全票价为240元/人,
(1)设学生人数为x,甲旅行社收费为y甲,乙旅行社收费为y乙,分别计算两家旅行社的收费(建立表达式).
(2)当学生人数为多少时,两家旅行社的收费一样?
(3)就学生人数讨论哪家旅行社更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:甲、乙两车分别从相距300千米的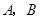 两地同时出发相向而行,其中甲到
两地同时出发相向而行,其中甲到 地后立即返回,下图是它们离各自出发地的距离
地后立即返回,下图是它们离各自出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.
(1)求甲车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围;
(2)当它们行驶到与各自出发地的距离相等时,用了 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式;
(小时)之间的函数关系式;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.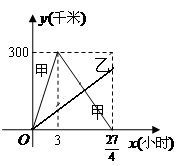
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.


(1)参照图象,求b、图②中c及d的值;
(2)连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为 ;
(3)当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)若点P、点Q在运动路线上相距的路程为25cm,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在直角坐标系中,设x轴为直线l,函数 的图像分别是
的图像分别是 ,半径为1的
,半径为1的 与直线
与直线 中的两条相切,例如
中的两条相切,例如 是其中一个
是其中一个 的圆心坐标.
的圆心坐标.
(1)写出其余满足条件的 的圆心坐标;
的圆心坐标;
(2)在图中标出所有圆心,并用线段依次连接各圆心,求所得几何图形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
甲、乙两车分别从A地将一批物品运往B地,再返回A地,如图表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回.请根据图象中的数据回答:
(1)甲车出发多长时间后被乙车追上?
(2)甲车与乙车在距离A地多远处迎面相遇?
(3)甲车从B地返回的速度多大时,才能比乙车先回到A地?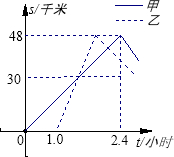
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数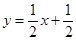 的图象与x轴交于点A,与y轴交于点B,与反比例函数
的图象与x轴交于点A,与y轴交于点B,与反比例函数 的图象在第一象限内交于点C,CD⊥x轴于点D,OD=2AO,求反比例函数
的图象在第一象限内交于点C,CD⊥x轴于点D,OD=2AO,求反比例函数 的表达式.
的表达式. 
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(-4,0),点P在射线AB上运动,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.
(1)求直线AB的函数解析式;
(2)当点P在线段AB(不包括A,B两点)上时.
①求证:∠BDE=∠ADP;
②设DE=x,DF=y.请求出y关于x的函数解析式;
(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com