
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,延长
的中点,延长![]() 至
至![]() ,使得
,使得![]() ,连接
,连接![]() 、
、![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)当![]() ,
,![]() 时,判断
时,判断![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)详见解析;(2)![]() 是底角为
是底角为![]() 的等腰三角形,解析解析
的等腰三角形,解析解析
【解析】
(1)由“ASA“可证△AEF≌△CED,可得AF=CD,根据邻边相等的平行四边形是菱形即可证明;
(2)由勾股定理可求AB的长,由中位线定理可求DF=DB=5,即可求解.
(1)∵AF∥CD,
∴∠EAF=∠ECD,
∵E是AC中点,
∴AE=EC,
在△AEF和△CED中,
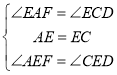
∴△AEF≌△CED(ASA),
∴AF=CD,
∴四边形AFCD是平行四边形,
∵∠ACB=![]() ,AD=DB,
,AD=DB,
∴CD=AD=BD,
∴四边形AFCD是菱形.
(2)∵∠ACB=![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴AB=![]()
∵点D,E分别是边AB,AC的中点,
∴BC=2DE,DB=![]() AB=5,
AB=5,
∵四边形AFCD是菱形,
∴DF=2DE=BC=5,
∴DF=DB,
∴△DFB是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=6,OC=4,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数 ![]() 的图象与BC边交于点E.
的图象与BC边交于点E.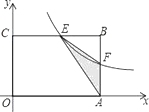
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
(1)有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.例如:![]() 的有理化因式是
的有理化因式是![]() ;
;![]() 的有理化因式是
的有理化因式是![]() .
.
(2)分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到去分母中根号的目的.如:![]() ,
,![]()
问题解决:
(1)填空:![]() 的有理化因式是______.(x≥1)
的有理化因式是______.(x≥1)
(2)直接写出下列各式分母有理化的结果:
①![]() _____;②
_____;②![]() ______.
______.
(3)计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家![]() 妈妈8:30从家出发,乘车沿相同路线去姥姥家
妈妈8:30从家出发,乘车沿相同路线去姥姥家![]() 在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是
在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是![]()
![]()
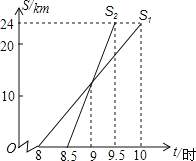
A. 9:00妈妈追上小亮B. 妈妈比小亮提前到达姥姥家
C. 小亮骑自行车的平均速度是![]() D. 妈妈在距家13km处追上小亮
D. 妈妈在距家13km处追上小亮
查看答案和解析>>
科目:初中数学 来源: 题型:
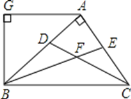
【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个一次函数与![]() 轴的交点关于
轴的交点关于![]() 轴对称,则称这两个一次函数为“对心函数”,这两个与
轴对称,则称这两个一次函数为“对心函数”,这两个与![]() 轴的交点为“对心点”.
轴的交点为“对心点”.

(1)写出一个![]() 的对心函数:________,这两个“对心点”为:_______;
的对心函数:________,这两个“对心点”为:_______;
(2)直线![]() 经过点
经过点![]() 和
和![]() ,直线
,直线![]() 的“对心函数”直线
的“对心函数”直线![]() 与
与![]() 轴的交点
轴的交点![]() 位于点
位于点![]() 的上方,且直线
的上方,且直线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 为直线
为直线![]() 的“对心点”.点
的“对心点”.点![]() 是动直线
是动直线![]() 上不与
上不与![]() 重合的一个动点,且
重合的一个动点,且![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)如图,直线![]() 与其“对心函数”直线
与其“对心函数”直线![]() 的交点
的交点![]() 位于第一象限,
位于第一象限,![]() 、
、![]() 分别为直线
分别为直线![]() 、
、![]() 的“对心点”,点
的“对心点”,点![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ;一动点
;一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 单位
单位![]() 秒的速度运动到点
秒的速度运动到点![]() ,再沿线段
,再沿线段![]() 以
以![]() 单位
单位![]() 秒的速度运动到点
秒的速度运动到点![]() 后停止,点
后停止,点![]() 在整个运动过程中所用最短时间为
在整个运动过程中所用最短时间为![]() 秒,求直线
秒,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办的”中国汉字听写大会“比赛受到各班的广泛关注,为了了解学生对”中国汉字听写大会“活动的喜爱程度,对部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为A类(非常喜欢),B类(较喜欢),C类(一般),D类(不喜欢).请结合两幅统计图,回答下列问题
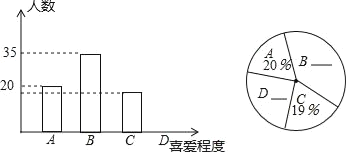
(1)写出本次抽样调查的总人数;
(2)请补全两幅统计图,写出计算过程;
(3)若该校有1500名学生.请你估计对“中国汉字听写大会”此项活动不喜欢的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备为七年级同学庆祝最后一个“儿童节”,至少需要甲种鲜花266朵,乙种鲜花169朵,制成A、B两种造型共16束.要求A造型用甲种鲜花18朵,乙种鲜花10朵;B造型用甲种鲜花16朵,乙种鲜花11朵,送某花店制作.
(1)花店共有几种制作方案?分别有哪几种?
(2)若A种造型每束鲜花可获得利润12元,B种造型每束鲜花可获得利润10元.如果你是店主,你选择哪种制作方案?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com