
【题目】如图,AC是⊙O的直径,PA切⊙O于点A,点B是⊙O上的一点,且∠BAC=30°,∠APB=60°.
(1)求证:PB是⊙O的切线;
(2)若⊙O的半径为2,求弦AB及PA,PB的长.
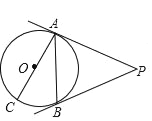
【答案】(1)见解析;(2)2
【解析】
试题(1)连接OB,证PB⊥OB.根据四边形的内角和为360°,结合已知条件可得∠OBP=90°得证;
(2)连接OP,根据切线长定理得直角三角形,根据含30度角的直角三角形的性质即可求得结果。
(1)连接OB.
∵OA=OB,∴∠OBA=∠BAC=30°.
∴∠AOB=80°-30°-30°=20°.
∵PA切⊙O于点A,∴OA⊥PA,
∴∠OAP=90°.
∵四边形的内角和为360°,
∴∠OBP=360°-90°-60°-20°=90°.
∴OB⊥PB.
又∵点B是⊙O上的一点,
∴PB是⊙O的切线.
(2)连接OP,
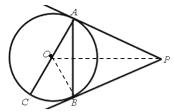
∵PA、PB是⊙O的切线,
∴PA=PB,∠OPA=∠OPB=![]() ,∠APB=30°.
,∠APB=30°.
在Rt△OAP中,∠OAP=90°,∠OPA=30°,
∴OP=2OA=2×2=4.
∴PA=OP2-OA2=2
∵PA=PB,∠APB=60°,
∴PA=PB=AB=2。


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】某农户承包荒山种植某产品种蜜柚![]() 已知该蜜柚的成本价为8元
已知该蜜柚的成本价为8元![]() 千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量
千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量![]() 千克
千克![]() 与销售单价
与销售单价![]() 元
元![]() 千克
千克![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
![]() 求y与x的函数关系式,并写出x的取值范围;
求y与x的函数关系式,并写出x的取值范围;
![]() 当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
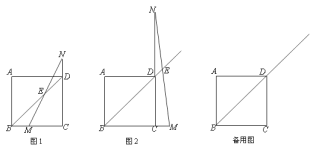
【题目】在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD-2DE=![]() BM;
BM;
(2)如图2,当点M在BC延长线上时,BD、DE、BM之间满足的关系式是什么?;
(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G.若DE=![]() ,且AF:FD=1:2时,求线段DG的长.
,且AF:FD=1:2时,求线段DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=![]() ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF

查看答案和解析>>
科目:初中数学 来源: 题型:
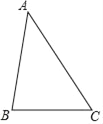
【题目】如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC、AB交于点D、E.
(1)在图中作出AB的垂直平分线DE,并连接BD.
(2)证明:△ABC∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(m+1)x|2m|﹣1 ,
①当m何值时,y是x的正比例函数?②当m何值时,y是x的反比例函数?
(上述两个问均要求写出解析式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )
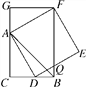
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为_____.
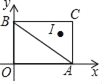
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com