
 如图,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y=
如图,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y=| 1 |
| 4 |
| 1 |
| 9 |
| AB |
| CD |
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地.两车同时出发,两车相遇时快车因机械小故障要将所有乘客转移到慢车上,转移乘客后慢车按原速改变方向立即驶向乙地.快车转移乘客后立即在原地用了2小时进行维修.然后按原速驶往乙地,结果两车同时到达终点,设行驶时间未x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行一下探究;
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地.两车同时出发,两车相遇时快车因机械小故障要将所有乘客转移到慢车上,转移乘客后慢车按原速改变方向立即驶向乙地.快车转移乘客后立即在原地用了2小时进行维修.然后按原速驶往乙地,结果两车同时到达终点,设行驶时间未x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行一下探究;查看答案和解析>>
科目:初中数学 来源: 题型:
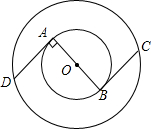 如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=
如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| a |
| b |
| ab |
| ab |
| ab |
| ab |
| ab |
| 1 |
| m |
查看答案和解析>>
科目:初中数学 来源: 题型:
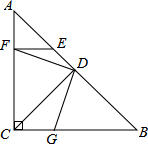 已知在△ABC中,∠ACB=90°,AC=BC,CD⊥AB,垂足为D,E是AB上一点,EF⊥AC,垂足为F,G是BC上一点,CG=EF,求证:DF=DG.
已知在△ABC中,∠ACB=90°,AC=BC,CD⊥AB,垂足为D,E是AB上一点,EF⊥AC,垂足为F,G是BC上一点,CG=EF,求证:DF=DG.查看答案和解析>>
科目:初中数学 来源: 题型:
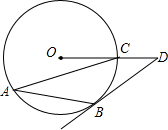 如图,AB、AC是⊙O的两条弦,过点B的切线与OC的延长线交于点D,若∠D=36°,则∠CAB的度数为( )
如图,AB、AC是⊙O的两条弦,过点B的切线与OC的延长线交于点D,若∠D=36°,则∠CAB的度数为( )| A、54° | B、44° |
| C、27° | D、22° |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com