
 如图,AB∥CD,EF、GH分别平分∠AEG和∠EGD,请问EF和GH平行吗?请说明理由.
如图,AB∥CD,EF、GH分别平分∠AEG和∠EGD,请问EF和GH平行吗?请说明理由. 分析 先由AB∥CD得到∠AEG=∠DGE,则利用角平分线定义得到∠FEG=$\frac{1}{2}$∠AEG,∠HGE=$\frac{1}{2}∠$DGE,则∠FEG=∠HGE,然后根据平行线的判定即可得到EF∥GH.
解答 解:EF∥GH.理由如下:
∵AB∥CD,
∴∠AEG=∠DGE,
∵EF、GH分别平分∠AEG和∠EGD,
∴∠FEG=$\frac{1}{2}$∠AEG,∠HGE=$\frac{1}{2}∠$DGE,
∴∠FEG=∠HGE,
∴EF∥GH.
点评 本题考查了平行线的判定与性质:平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校操场旁边一棵水杉树被大风吹断,如图测得树顶与水平地面刚好成60度夹角,且离树的底端5米,求这棵树原来有多高?(结果保留整数,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
学校操场旁边一棵水杉树被大风吹断,如图测得树顶与水平地面刚好成60度夹角,且离树的底端5米,求这棵树原来有多高?(结果保留整数,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
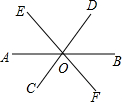 直线AB,CD,EF相交于点O,如图.
直线AB,CD,EF相交于点O,如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是边长为1的六个小正方形组成的平面图形,经过折叠能围成一个正方体,那么点A、B在围成的正方体上相距( )
如图是边长为1的六个小正方形组成的平面图形,经过折叠能围成一个正方体,那么点A、B在围成的正方体上相距( )| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com