
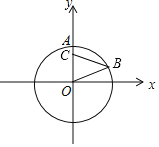
【题目】如图,半径为5的⊙O与y轴相交于A点,B为⊙O在x轴上方的一个动点(不与点A重合),C为y轴上一点且∠OCB=60°,I为△BCO的内心,则△AIO的外接圆的半径的取值(或取值范围)为_____.
【答案】![]()
【解析】
首先证明∠AIO=120°=定值,OA=5=定值,推出点G的运动轨迹是![]() ,推出△AOI的外接圆的半径是定值,由此即可解决问题.
,推出△AOI的外接圆的半径是定值,由此即可解决问题.
如图,
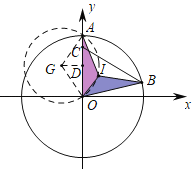
∵∠BCO=60°,
∴∠CBO+∠COB=120°,
∵I是内心,
∴∠IOB=![]() ∠COB,∠IBO=
∠COB,∠IBO=![]() ∠CBO,
∠CBO,
∴∠IOB+∠IBO=![]() (∠COB+CBO)=60°,
(∠COB+CBO)=60°,
∴∠OIB=180°﹣∠IOB﹣∠IBO=120°,
∵OA=OB,∠AOI=∠BOI,OI=OI,
∴△AIO≌△BOI(SAS),
∴∠AIO=∠BIO=120°,
作△AOI的外接圆⊙G,连接AG,OG,作GD⊥OA于D.
∵∠AIO=120°=定值,OA=5=定值,
∴点G的运动轨迹是![]() ,
,
∴△AOI的外接圆的半径是定值,
∵GA=GO,GD⊥OA,∠AGO=120°,
∴∠AGD=![]() ∠AGO=120°,AD=OD=
∠AGO=120°,AD=OD=![]() ,
,
∴AG=![]() =
=![]() =
=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
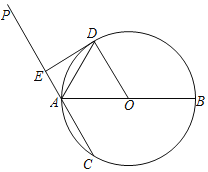
【题目】如图,AB是⊙O的直径,过点A的直线PC交⊙O于A,C两点,AD平分∠PAB,射线AD交⊙O于点D,过点D作DE⊥PA于点E.
(1)求证:ED为⊙O的切线;
(2)若AB=10,ED=2AE,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
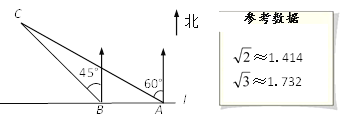
【题目】如图,同学们利用所学知识去测量海平面上一个浮标到海岸线的距离. 在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,小宇同学在A处观测得浮标在北偏西60°的方向,小英同学在距点A处60米远的B点测得浮标在北偏西45°的方向,求浮标C到海岸线l的距离(结果精确到0.01 m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,∠A=40°,∠B=60°,当∠BCD=40°时,证明:CD为△ABC的完美分割线.
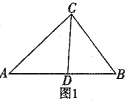
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD是以AC为底边的等腰三角形,求∠ACB的度数.
(3)如图2,在△ABC中,AC=2,BC=2,CD是△ABC的完美分割线,△ACD是以CD为底边的等腰三角形,求CD的长.
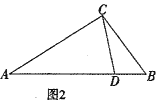
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生在一起射击训练中,随机抽取10名学生的成绩如下表,回答问题:
环数 | 6 | 7 | 8 | 9 |
人数 | 1 | 5 | 2 |
|
(1)填空:![]() _______;
_______;
(2)10名学生的射击成绩的众数是_______环,中位数是_______环;
(3)若9环(含9环)以上评为优秀射手,试估计全年级500名学生中有_______名是优秀射手.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=mx2+nx﹣3(m≠0)与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,直线y=﹣x与该抛物线交于E,F两点.
(1)求点C坐标及抛物线的解析式.
(2)P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值.
(3)以点C为圆心,1为半径作圆,⊙C上是否存在点D,使得△BCD是以CD为直角边的直角三角形?若存在,直接写出D点坐标;若不存在,请说明理由.
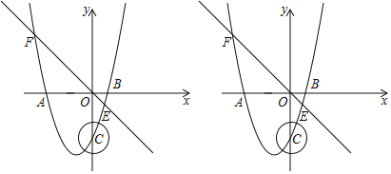
查看答案和解析>>
科目:初中数学 来源: 题型:
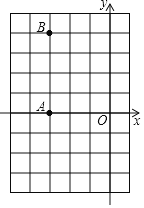
【题目】坐标为整数的点叫格点,如图,已知A(-3,0)、B(-3,4)和原点都是格点,在如图6×9的网格中使用无刻度的直尺按要求作图.
(1)找格点C,连BC,使BC与OA的交点就是OA的中点,画出图形直接写出C点坐标.
(2)按以下方法可以作出∠AOB的平分线.
第一步:找格点D,使OD=OB;
第二步:找格点E,使DE⊥OB交AB于F;
第三步:连OF,则OF是∠AOB的平分线;
请你按步骤完成作图,并写出D、E三点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,点M是BC的中点.
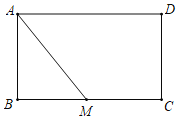
(1)在AM上求作一点E,使△ADE∽△MAB(尺规作图,不写作法);
(2)在(1)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
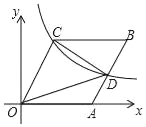
【题目】如图,菱形OABC的一OA在x轴的正半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,则△COD的面积为_____.
的图象经过点C,与AB交于点D,则△COD的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com