
| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
分析 可以设水池有水为x升,泉每天流水y升,A型抽水机每台每天抽水z升,根据24部A型抽水机6天可抽干池水,若用21部A型抽水机8天也可抽干池水可列出两个关于未知数的方程,求方程组的解可得到yz之间的关系,即可得解.
解答 解:假设水池有水为x升,泉每天流水y升,A型抽水机每台每天抽水z升.
则:$\left\{\begin{array}{l}{x+6y=24×6z}\\{x+8y=21×8z}\end{array}\right.$,
解得:y=12z.
即泉水每天的流量相当于12台抽水机的流量,用12台抽水机抽水那么池永远抽不干的.
故选:B.
点评 本题考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 年龄组 | 13岁 | 14岁 | 15岁 | 16岁 |
| 参赛人数 | 5 | 19 | 12 | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,EF=2,则△CEF的周长为( )
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,EF=2,则△CEF的周长为( )| A. | 8 | B. | 9.5 | C. | 10 | D. | 11.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
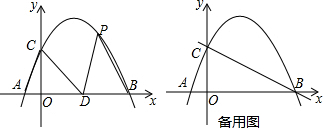
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
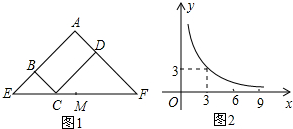
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
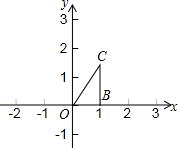 已知:如图,在平面直角坐标系xOy中,点B1、点C1的坐标分别为(1,0),(1,$\sqrt{3}$).将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OBnCn.
已知:如图,在平面直角坐标系xOy中,点B1、点C1的坐标分别为(1,0),(1,$\sqrt{3}$).将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OBnCn.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com