
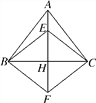
【题目】如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据题意可证得△BCE为等腰三角形,由AH⊥CB,则BH=HC,从而得出四边形EBFC是菱形;
(2)由(1)得∠2=∠3,再根据∠BAC=∠ECF,得∠4=∠3,由AH⊥CB,得∠3+∠1+∠2=90°,从而得出AC⊥CF.
试题解析:证明:(1)∵AB=AC,AH⊥CB,
∴BH=HC.
∵FH=EH,
∴四边形EBFC是平行四边形.
又∵AH⊥CB,
∴四边形EBFC是菱形.
(2)证明:如图,
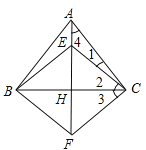
∵四边形EBFC是菱形.
∴∠2=∠3=![]() ∠ECF.
∠ECF.
∵AB=AC,AH⊥CB,
∴∠4=![]() ∠BAC.
∠BAC.
∵∠BAC=∠ECF
∴∠4=∠3.
∵AH⊥CB
∴∠4+∠1+∠2=90°.
∴∠3+∠1+∠2=90°.
即:AC⊥CF.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: .
.
请结合题意,完成本题的解答.
(1)解不等式①,得 ,依据是: .
(2)解不等式③,得 .
(3)把不等式①,②和③的解集在数轴上表示出来.
![]()
(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
查看答案和解析>>
科目:初中数学 来源: 题型:
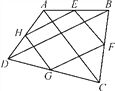
【题目】如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.
(1)当四边形ABCD是矩形时,四边形EFGH是_________,请说明理由;
(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN,EF是两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,则∠1=∠2.
(1)用尺规作图作出镜面BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系;
(3)你是如何思考的?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一副直角三角板放在同一条直线AB上,其中![]() ,
,![]() .
.
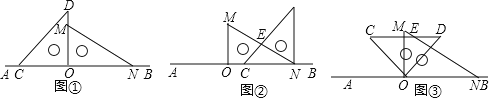
![]() 将图1中的三角尺OCD沿AB的方向平移至图
将图1中的三角尺OCD沿AB的方向平移至图![]() 的位置,使得点O与点N重合,CD与MN相交于点E,求
的位置,使得点O与点N重合,CD与MN相交于点E,求![]() 的度数;
的度数;
![]() 将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在
将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在![]() 的内部,如图3,且OD恰好平分
的内部,如图3,且OD恰好平分![]() ,CD与MN相交于点E,求
,CD与MN相交于点E,求![]() 的度数;
的度数;
![]() 将图1中的三角尺OCD绕点O按每秒
将图1中的三角尺OCD绕点O按每秒![]() 的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直
的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直![]() 直接写出结果
直接写出结果![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
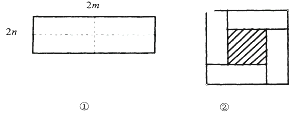
(1)你认为图②中的阴影部分的正方形的边长等于_________________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①_________________________________________________________.
方法②_________________________________________________________.
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式间的等量关系吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com