
【题目】如图所示,直线![]() 与坐标轴交于点
与坐标轴交于点![]() ,与抛物线
,与抛物线![]() 交于点
交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)求抛物线的解析式;
(2)若点![]() 是线段
是线段![]() 上(不与
上(不与![]() 重合)的一个动点,过点
重合)的一个动点,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,以
,以![]() 为边作矩形
为边作矩形![]() ,请求出矩形
,请求出矩形![]() 周长的最大值;
周长的最大值;
(3)若点![]() 在
在![]() 轴正半轴上,当
轴正半轴上,当![]() 恰好是等腰三角形时,请直接写出点
恰好是等腰三角形时,请直接写出点![]() 的坐标.
的坐标.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]()
【解析】
(1)对于![]() ,令y=0求出x=-2即可得点A(-2,0),把A,C点坐标代入
,令y=0求出x=-2即可得点A(-2,0),把A,C点坐标代入![]() 求出a,c的值即可;
求出a,c的值即可;
(2)设点D的坐标是![]() ,则点E的坐标是
,则点E的坐标是![]() ,可得DE=
,可得DE=![]() ,证明△DFE∽△BOA,得DF∶EF∶DE =3∶4∶5.从而可得矩形DFEG的周长
,证明△DFE∽△BOA,得DF∶EF∶DE =3∶4∶5.从而可得矩形DFEG的周长![]() ,从而可得结论;
,从而可得结论;
(3)由勾股定理求出AC=![]() ,设P(0,m)(m>0),然后分AP=AC,AC=PC,AP=PC三种情况列式求解即可.
,设P(0,m)(m>0),然后分AP=AC,AC=PC,AP=PC三种情况列式求解即可.
解:(1)由![]() 知,y=0时x=-2,
知,y=0时x=-2,
∴A(-2,0).
∵抛物线![]() 经过A(-2,0) 、C(4,
经过A(-2,0) 、C(4,![]() )两点,
)两点,
∴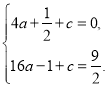 解得
解得
∴抛物线的解析式为![]() .
.
(2)∵DE∥y轴,点D在线段AC上,点E在抛物线上,
∴设点D的坐标是![]() ,则点E的坐标是
,则点E的坐标是![]() .
.
∴DE=![]() .
.
由![]() 知A(-2,0),B(0,
知A(-2,0),B(0, ![]() ),
),
∴AO=2,OB=![]()
Rt△OAB中,由勾股定理可得,AB=![]()
∴OB∶OA∶AB =3∶4∶5.
由题意得,∠DFE=∠BOA=90°,∠EDF=∠ABO,
∴△DFE∽△BOA.
∴DF∶EF∶DE =3∶4∶5.
∴矩形DFEG的周长![]() ,其中
,其中![]() .
.
∴当![]() 时,矩形DFEG的周长取得最大值
时,矩形DFEG的周长取得最大值![]() .
.
(3)由题意得,![]() ,
,![]() ,
,
设![]() ,
,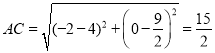
①若![]() ,则
,则![]()
![]()
![]()
![]() 或
或![]() (舍去)
(舍去)
②若![]() ,则
,则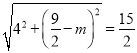
![]()
![]()
![]() 或
或![]() (负值舍去)
(负值舍去)
③若![]() ,则
,则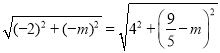
![]()
![]()
综上所述,点P的坐标为![]() ,
,![]() ,
,![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 点
点![]() 是直线
是直线![]() 上的一动点(不与点
上的一动点(不与点![]() 重合),连接
重合),连接![]() 在
在![]() 的右侧以
的右侧以![]() 为斜边作等腰直角三角形
为斜边作等腰直角三角形![]() .点
.点![]() 是
是![]() 的中点,连接
的中点,连接![]() .
.
[问题发现]
(1)如图(1),当点![]() 是
是![]() 的中点时,线段
的中点时,线段![]() 与
与![]() 的数量关系是______,
的数量关系是______,![]() 与
与![]() 的位置关系是______;
的位置关系是______;
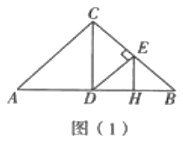
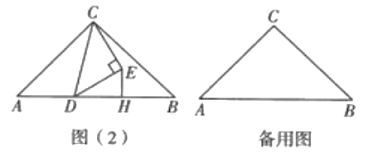
[猜想论证]
(2)如图(2),当点![]() 在边
在边![]() 上且不是
上且不是![]() 的中点时,(1)中的结论是否仍然成立?若成立,请仅就图(2)中的情况给出证明;若不成立,请说明理由.
的中点时,(1)中的结论是否仍然成立?若成立,请仅就图(2)中的情况给出证明;若不成立,请说明理由.
[拓展应用]
(3)若![]() ,其他条件不变,连接
,其他条件不变,连接![]() .当
.当![]() 是等边三角形时,请直接写出
是等边三角形时,请直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着网络资源日趋丰富,更多人选择在线自主学习,在线学习方式有在线阅读、在线听课、在线答题、在线讨论.济川中学初二年级随机抽取部分学生进行“你对哪类在线学习方式最感兴趣”的调查(每位同学只能选一项),并根据调查结果绘制成如下两幅不完整的统计图.根据图中信息,解答下列问题:
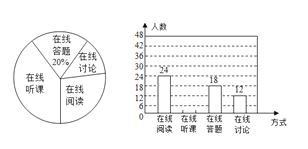
(1)补全条形统计图;
(2)求扇形统计图中“在线阅读”对应的扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校体育社团活动计划开设“足球、篮球、排球、乒乓球”四个体育兴趣小组,每个学生只能选报一项参加活动,为了解该社团成员选择兴趣小组的情况,某调查小组在社团中进行了一次抽样调查,绘制了如下尚不完整的统计图表.
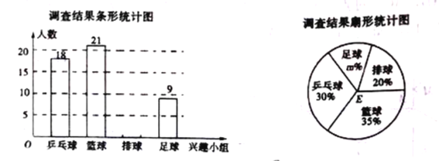
根据以上信息解答下列问题:
(1)本次抽样调查的样本容量为 ,扇形统计图中的值为 .
(2)补全条形统计图;
(3)若该学校有学生![]() 人,有
人,有![]() 的学生选择了参加体育社团活动,请你估计该校选择排球和足球这两个兴趣小组的学生大约共有多少人?
的学生选择了参加体育社团活动,请你估计该校选择排球和足球这两个兴趣小组的学生大约共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售某种品牌的空调和电风扇:
(1)已知购进8台空调和20台电风扇共需17400元,购进10台空调和30台电风扇共需22500元,求每台空调和电风扇的进货价;
(2)已知空调标价为2500元/台,电风扇标价为250元/台.若商场购进空调和电风扇共60台,并全部打八折出售,设其中空调的数量为a台,商场通过销售这批空调和电风扇获得的利润为w元,求w和a之间的函数关系式;
(3)在(2)的条件下,若这批空调和电风扇的进货价不超过45300元,商场通过销售这批空调和电风扇获得的利润又不低于6000元,问商场共有多少种不同的进货方案,哪种进货方案获得的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,![]() 月
月![]() 日是母亲节,浩浩去花店买花送给母亲,挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花,已知康乃馨每支
日是母亲节,浩浩去花店买花送给母亲,挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花,已知康乃馨每支![]() 元,兰花每支
元,兰花每支![]() 元,浩浩只有
元,浩浩只有![]() 元,还想留着
元,还想留着![]() 元购买卡片.希望购买花的支数为
元购买卡片.希望购买花的支数为![]() 支,其中至少有一支是兰花.浩浩一共有多少种可能的购买方案?列出所有方案.
支,其中至少有一支是兰花.浩浩一共有多少种可能的购买方案?列出所有方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() ,已知
,已知![]() ,抛物线的对称轴交
,抛物线的对称轴交![]() 轴于点
轴于点![]() .
.
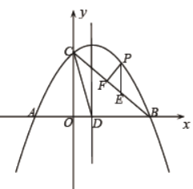
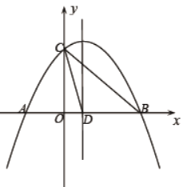
备用图
(1)求该抛物线的解析式;
(2)连接![]() ,能否在抛物线上找到一点
,能否在抛物线上找到一点![]() ,使得
,使得![]() ,若有求
,若有求![]() 点的坐标,若没有说明理由;
点的坐标,若没有说明理由;
(3)若点![]() 为
为![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当
,当![]() 的周长最大时,求点
的周长最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com