
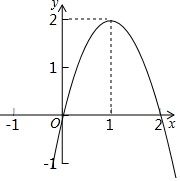
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题.分析 (1)找到抛物线与x轴的交点,即可得出方程ax2+bx+c=0的两个根;
(2)找出抛物线在x轴下方时,x的取值范围即可;
(3)根据图象可以看出k取值范围.
解答 解:(1)由图象可得:x1=0,x2=2;
(2)结合图象可得:x<0或x>2时,y<0,
即不等式ax2+bx+c<0的解集为x<0或x>2;
(3)根据图象可得,k>2时,方程ax2+bx+c=k没有实数根.
点评 本题主要考查了二次函数的图象与方程和不等式的关系,求方程ax2+bx+c=0的两个根,即为抛物线与x轴的交点的横坐标;判断y>0,y=0,y<0时,x的取值范围,要结合开口方向,图象与x轴的交点而定;方程ax2+bx+c=k有无实数根,看顶点坐标的纵坐标即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 月份 | 一 | 二 | 三 | 四 | 五 | 六 |
| 实际月销售(辆) | 24 | 19 | 22 | 23 | ||
| 比计划月销售量增(辆) | +4 | -2 | 0 | +3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
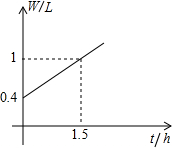 水龙头关闭不严就会滴水,现在没拧紧的水龙头下面放一个容器,容器内的盛水量W(L)与滴水时间t(h)的关系如图所示,给合图象解答下列问题:
水龙头关闭不严就会滴水,现在没拧紧的水龙头下面放一个容器,容器内的盛水量W(L)与滴水时间t(h)的关系如图所示,给合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的一条弦,C,D是⊙O上的两个动点,且在AB弦的异侧,连接CD.
如图,AB是⊙O的一条弦,C,D是⊙O上的两个动点,且在AB弦的异侧,连接CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com