
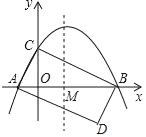
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,2)
(1)求抛物线的表达式;
(2)抛物线的对称轴与x轴交于点M,点D与点C关于点M对称,试问在该抛物线的对称轴上是否存在点P,使△BMP与△ABD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)满足条件的点P的坐标为(
x+2;(2)满足条件的点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,5)或(
,5)或(![]() ,﹣5).
,﹣5).
【解析】
(1)利用待定系数法求抛物线的表达式;
(2)使△BMP与△ABD相似的有三种情况,分别求出这三个点的坐标.
(1)∵抛物线与x轴交于点A(﹣1,0),B(4,0),
∴设抛物线的解析式为y=a(x+1)(x﹣4),
∵抛物线与y轴交于点C(0,2),
∴a×1×(﹣4)=2,
∴a=﹣![]()
![]() ,
,
∴抛物线的解析式为y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)如图1,连接CD,∵抛物线的解析式为y=﹣![]() x2+
x2+![]() x+2,
x+2,
∴抛物线的对称轴为直线x=![]() ,
,
∴M(![]() ,0),∵点D与点C关于点M对称,且C(0,2),
,0),∵点D与点C关于点M对称,且C(0,2),
∴D(3,﹣2),
∵MA=MB,MC=MD,
∴四边形ACBD是平行四边形,
∵A(﹣1,0),B(4,0),C(3,﹣22),
∴AB2=25,BD2=(4﹣1)2+22=5,AD2=(3+1)2+22=20,
∴AD2+BD2=AB2,
∴△ABD是直角三角形,
∴∠ADB=90°,
设点P(![]() ,m),
,m),
∴MP=|m|,
∵M(![]() ,0),B(4,0),
,0),B(4,0),
∴BM=![]() ,
,
∵△BMP与△ABD相似,
∴①当△BMP∽ADB时,
∴![]() ,
,
∴![]() ,
,
∴m=±![]() ,
,
∴P(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ),
),
②当△BMP∽△BDA时,
![]() ,
,
∴![]() ,
,
∴m=±5,
∴P(![]() ,5)或(
,5)或(![]() ,﹣5),
,﹣5),
即:满足条件的点P的坐标为P(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,5)或(
,5)或(![]() ,﹣5).
,﹣5).


科目:初中数学 来源: 题型:
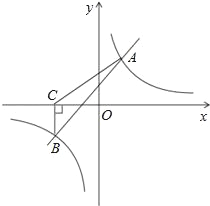
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
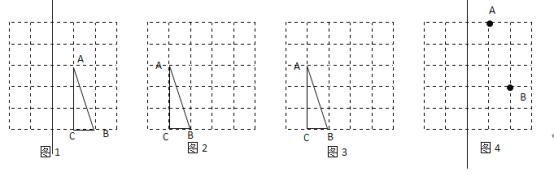
【题目】如图是由边长为![]() 的小正方形构成的网格,每个小正方形的顶点叫做格点,
的小正方形构成的网格,每个小正方形的顶点叫做格点,![]() 的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
(1)如图![]() ,作
,作![]() 关于直线
关于直线![]() 的对称图形
的对称图形![]() ;
;
(2)如图![]() ,作
,作![]() 的高
的高![]() ;
;
(3)如图![]() ,作
,作![]() 的中线
的中线![]() ;
;
(4)如图![]() ,在直线
,在直线![]() 上作出一条长度为
上作出一条长度为![]() 个单位长度的线段
个单位长度的线段![]() 在
在![]() 的上方
的上方![]() ,使
,使![]() 的值最小.
的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬学生爱国主义精神,充分展现新时期青少年良好的思想道德素质和精神风貌,丰富学生的校园生活,陶冶师生的情操,某校举办了“中国梦爱国情成才志”中华经典诗文诵读比赛.九(1)班通过内部初选,选出了丽丽和张强两位同学,但学校规定每班只有1个名额,经过老师与同学们商量,用所学的概率知识设计摸球游戏决定谁去,设计的游戏规则如下:在A、B两个不透明的箱子分别放入黄色和白色两种除颜色外均相同的球,其中A箱中放置3个黄球和2个白球;B箱中放置1个黄球,3个白球,丽丽从A箱中摸一个球,张强从B箱摸一个球进行试验,若两人摸出的两球都是黄色,则丽丽去;若两人摸出的两球都是白色,则张强去;若两人摸出球颜色不一样,则放回重复以上动作,直到分出胜负为止.
根据以上规则回答下列问题:
(1)求一次性摸出一个黄球和一个白球的概率;
(2)判断该游戏是否公平?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若正整数k满足个位数字为1,其他数位上的数字均不为1且十位与百位上的数字相等,
我们称这样的数k为“言唯一数”,交换其首位与个位的数字得到一个新数k',并记F(k)=![]() .
.
(1)最大的四位“言唯一数”是 ,最小的三位“言唯一数”是 ;
(2)证明:对于任意的四位“言唯一数”m,m+m'能被11整除;
(3)设四位“言唯一数”n=1000x+100y+10y+1(2≤x≤9,0≤y≤9且y≠1,x、y均为整数),若F(n)仍然为“言唯一数”,求所有满足条件的四位“言唯一数”n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.

(1)①如图2,求出抛物线![]() 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线![]() 与
与![]() 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线![]() 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线![]() 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且![]() 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.

(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com