
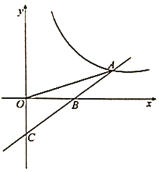
【题目】如图,直线y=4﹣x与双曲线y![]() 交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA为直径的圆与直线BC的交点坐标是_____.
交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA为直径的圆与直线BC的交点坐标是_____.
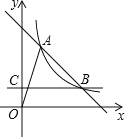
【答案】(﹣1,1)和(2,1).
【解析】
求得交点A、B的坐标,即可求得直径AB的长度和P点的坐标,从而求得PE的长度,利用勾股定理求得EM=EN=![]() ,结合P的坐标即可求得以OA为直径的圆与直线BC的交点坐标.
,结合P的坐标即可求得以OA为直径的圆与直线BC的交点坐标.
由 求得
求得![]() 或
或![]() ,
,
∴A(1,3),B(3,1),
∴OA![]() ,
,
设OA的中点为P,以AB为直径的⊙P与直线BC的交点为M、N,
过P点作PD⊥x轴于D,交BC于E,连接PN,
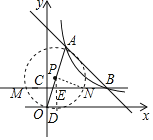
∵P是OA的中点,
∴P(![]() ,
,![]() ),
),
∴PD![]() ,
,
∵BC⊥y轴,垂足为C,
∴BC∥x轴,
∴PD⊥BC,
∴PE![]() 1
1![]() ,
,
在Rt△PEN中,EM=EN![]() ,
,
∴M(﹣1,1),N(2,1).
∴以OA为直径的圆与直线BC的交点坐标是(﹣1,1)和(2,1),
故答案为(﹣1,1)和(2,1).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图所示.
(元)符合一次函数关系,如图所示.
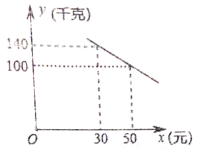
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若在销售过程中每天还要支付其他费用500元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,破残的圆形轮片上,弦AB的垂直平分线交AB于C,交弦AB于D.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)若AB=24cm,CD=8cm,求(1)中所作圆的半径.
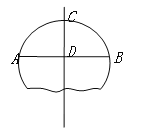
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐至县城有两座远近闻名的南北古塔,清朝道光11年至13年(公元1831--1833年)修建,南塔名为“文运塔”,高30米;北塔名为“凌云塔”.为了测量北塔的高度AB,身高为1.65米的小明在C处用测角仪CD,(如图所示)测得塔顶A的仰角为45°,此时小明在太阳光线下的影长为1.1米,测角仪的影长为1米.随后,他再向北塔方向前进14米到达H处,又测得北塔的顶端A的仰角为60°,求北塔AB的高度.(参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别交x轴,y轴于A(4.0),B(0,2)两点,与反比例函数y=![]() 的图象交于C.D两点,CE⊥x轴于点E且CE=3.
的图象交于C.D两点,CE⊥x轴于点E且CE=3.
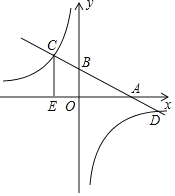
(1)求反比例函数与一次函数的解析式;
(2)根据图象直接写出:不等式0<kx+b<![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行,某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出50辆;若每辆自行车每降价20元,每月可多售出5辆,求该型号自行车降价多少元时,每月可获利30000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+5ax+c(a<0)与x轴负半轴交于A、B两点(点A在点B的左侧),与y轴交于C点,D是抛物线的顶点,过D作DH⊥x轴于点H,延长DH交AC于点E,且S△ABD:S△ACB=9:16,

(1)求A、B两点的坐标;
(2)若△DBH与△BEH相似,试求抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com