
 如图,AB∥CD∥EF,则下列各式中正确的是( )
如图,AB∥CD∥EF,则下列各式中正确的是( )| A. | ∠1=180°-∠3 | B. | ∠1=∠3-∠2 | C. | ∠2+∠3=180°-∠1 | D. | ∠2+∠3=180°+∠1 |
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=-5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 机场 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A机场 | 15 | 20 |
| B机场 | 10 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
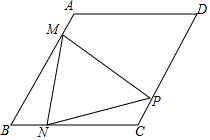 在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.
在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
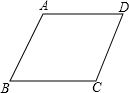 如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应添加的一个条件是AD=BC(或AB∥CD或∠A=∠C或∠B=∠D).
如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应添加的一个条件是AD=BC(或AB∥CD或∠A=∠C或∠B=∠D).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com