
分析 通过分析前几项的结果 $\frac{3}{4}$,$\frac{4}{6}$=$\frac{2}{3}$,$\frac{5}{8}$得出第n项结果为$\frac{n+1}{2n}$,再分析通项1-$\frac{1}{{n}^{2}}$=$\frac{n-1}{n}$•$\frac{n+1}{n}$,求出n项之积得出规律进行计算.
解答 解:(1)1-$\frac{1}{{2}^{2}}$=$\frac{3}{4}$;
(2))(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)=$\frac{2}{3}$;
(3)原式=$\frac{5}{8}$;
故答案为$\frac{3}{4}$;$\frac{2}{3}$;$\frac{5}{8}$;
(4)原式=$\frac{1}{2}$•$\frac{3}{2}$•$\frac{2}{3}$•$\frac{4}{3}$…$\frac{n-1}{n}$•$\frac{n+1}{n}$=$\frac{n+1}{2n}$.
点评 此题考查了分析代数式规律的能力,并对代数式进行化简求积.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
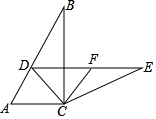 如图,在Rt△ABC 中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转,得到△DEC,若点D刚好落在AB边上,取DE边的中点F,连接FC,判断四边形ACFD的形状,并说明理由.
如图,在Rt△ABC 中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转,得到△DEC,若点D刚好落在AB边上,取DE边的中点F,连接FC,判断四边形ACFD的形状,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 水银柱的长度x(cm) | 4.0 | … | 8.0 | 9.6 |
| 体温计的度数y(℃) | 35.0 | … | 40.0 | 42.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5≤a<6 | B. | 5<a≤6 | C. | 5<a<6 | D. | 5≤a≤6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
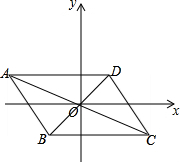 如图,已知点A(-4,2)、B(-1,-2),平行四边形ABCD的对角线交于坐标原点O.
如图,已知点A(-4,2)、B(-1,-2),平行四边形ABCD的对角线交于坐标原点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
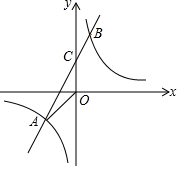 如图,已知B(1,4),A(n,-2)是反比例函数y=$\frac{m}{x}$的图象和一次函数y=kx+b的图象的两个交点,直线AB与y轴交于点C.
如图,已知B(1,4),A(n,-2)是反比例函数y=$\frac{m}{x}$的图象和一次函数y=kx+b的图象的两个交点,直线AB与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使30%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是( )
为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使30%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是( )| A. | ①④ | B. | ③④ | C. | ①③ | D. | ①② |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com