
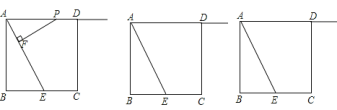
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 在射线
在射线![]() 上,过
上,过![]() 作
作![]() 于
于![]() ,设
,设![]() .
.
(1)求证:![]() ;
;
(2)当![]() 也是
也是![]() 边中点时,求
边中点时,求![]() 的值;
的值;
(3)若以![]() ,
,![]() ,
,![]() 为顶点的三角形也与
为顶点的三角形也与![]() 相似,试求
相似,试求![]() 的值;
的值;
(4)当点![]() 与点
与点![]() 重合时,设
重合时,设![]() 交
交![]() 于点
于点![]() ,试判断
,试判断![]() 与
与![]() 的大小关系并说明理由.
的大小关系并说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() ;(4)
;(4)![]() .
.
【解析】
(1)先证明∠PAF=∠AEB,再由∠PFA=∠ABE=90°,即可证出△PFA∽△ABE.
(2)当P是AD的中点时,AP=2,由△PFA∽△ABE,由相似三角形对应边成比例即可得出结论;
(3)分两种情况:当△EFP∽△ABE时,则PE∥AB,得出四边形ABEP为矩形.求出PA=EB=2,即x=2;当△PFE∽△ABE,且∠PEF=∠AEB时,先求出∠PAF=∠AEB,得到PE=PA ,再由勾股定理得出AE的长,再得出EF的长,根据相似三角形的性质求出PE的长,即可得出结论;
(4)先证明△ECG∽△ABE,求出CG、EG,再证明△AEG∽△ABE,即可得出∠GAE=∠BAE.
(1)∵四边形ABCD是正方形,∴AD∥BC,AB=BC=AD=4,∴∠ABE=90°,∠PAF=∠AEB.
又∵PF⊥AE,∴∠PFA=∠ABE=90°,∴△PFA∽△ABE.
(2)当P是AD的中点时,AP=2.
∵△PFA∽△ABE,∴![]() ,即
,即![]() ,∴AF
,∴AF![]() ;
;
(3)分两种情况:
①当△EFP∽△ABE,且∠PEF=∠EAB时,则有PE∥AB,∴四边形ABEP为矩形,∴PA=EB=2,即x=2.
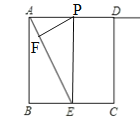
②当△PFE∽△ABE,且∠PEF=∠AEB时.
∵∠PAF=∠AEB,∴∠PEF=∠PAF,∴PE=PA.
∵PF⊥AE,∴点F为AE的中点.
∵AE![]() ,∴EF
,∴EF![]()
![]() ,即
,即![]() ,∴PE=5,∴AP=5,即x=5;
,∴PE=5,∴AP=5,即x=5;
∴满足条件的x的值为2或5;
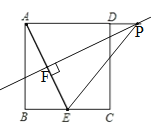
(4)∠GAE=∠BAE.理由如下:
如图,∵四边形ABCD是正方形,∴∠B=∠C=90°,AB=BC=4,∴∠BAE+∠AEB=90°.
∵E是BC的中点,∴BE=CE=2,∴AE![]() .
.
∵PE⊥AE,∴∠AEP=90°,∠AEB+∠CEG=90°,∴∠CEG=∠BAE,∴△ECG∽△ABE,∴![]() ,即
,即![]() ,∴CG=1,∴EG
,∴CG=1,∴EG![]()
![]() ,∴
,∴![]() .
.
又∵∠AEP=∠B=90°,∴△AEG∽△ABE,∴∠GAE=∠BAE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、C的坐标分别为(4,6)、(5,4),且AB平行于x轴,将矩形ABCD向左平移,得到矩形A′B′C′D′.若点A′、C′同时落在函数![]() 的图象上,则k的值为( )
的图象上,则k的值为( )
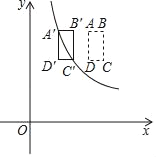
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长20米的篱笆围成一个一面靠墙的长方形的菜园,设菜园的宽为x米,面积为y平方米.
(1)求y与x的函数关系式及自变量的取值范围;
(2)怎样围才能使菜园的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
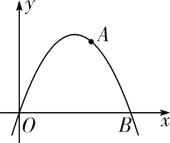
【题目】已知二次函数的解析式为y=-x2+4x,该二次函数交x轴于O、B两点,A为抛物线上一点,且横纵坐标相等(原点除外),P为二次函数上一动点,过P作x轴垂线,垂足为D(a,0)(a>0),并与直线OA交于点C.
(1)求A、B两点的坐标;
(2)当点P在线段OA上方时,过P作x轴的平行线与线段OA相交于点E,求△PCE周长的最大值及此时P点的坐标;
(3)当PC=CO时,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,关于![]() 的分式方程
的分式方程![]() .
.
(1)当![]() ,
,![]() 时,求分式方程的解;
时,求分式方程的解;
(2)当![]() 时,求
时,求![]() 为何值时分式方程
为何值时分式方程![]() 无解:
无解:
(3)若![]() ,且
,且![]() 、
、![]() 为正整数,当分式方程
为正整数,当分式方程![]() 的解为整数时,求
的解为整数时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=![]() 的图象上,若点A的坐标为(﹣2,﹣3),则k的值为( )
的图象上,若点A的坐标为(﹣2,﹣3),则k的值为( )
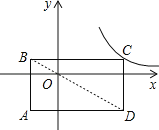
A. 1 B. ﹣5 C. 4 D. 1或﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
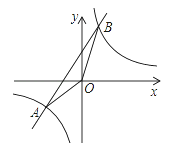
【题目】如图,已知A(﹣2,﹣2)、B(n,4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com