
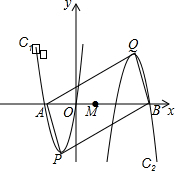
 如图,抛物线C1:y1=ax2+2ax(a>0)与x轴交于点A,顶点为点P.
如图,抛物线C1:y1=ax2+2ax(a>0)与x轴交于点A,顶点为点P.分析 (1)将抛物线的一般形式化为顶点式,即可得出结论;
(2)①先求出点A的坐标,即可确定出AM,即可得出结论;
②先求出点B的坐标,进而表示出AP,BP,分三种情况建立方程求解即可;
③先得到四边形APBQ为平行四边形,再由矩形判断出△APH∽△PBH即可得出a2=2m+3,即可解答此题.
解答 解:(1)∵抛物线C1:y1=ax2+2ax=a(x+1)2-a,
∴x=-1,P(-1,-a)
故答案为:直线x=-1,(-1,-a),
(2)①由旋转知,MA=MB,
当y1=0时,x1=-2,x2=0,
∴A(-2,0),
∴AO=2,
∵M(1,0),
∴AM=3,
∴AB=2MA=2×3=6;
②∵A(-2,0),AB=6,
∴B(4,0)
∵A(-2,0),P(-1,-a),
∴$AP=\sqrt{{1^2}+{{(-a)}^2}}=\sqrt{1+{a^2}}$,
$BP=\sqrt{25+{a^2}}$
当AB=AP时,1+a2=62,解得:$a=\sqrt{35}$(负值已舍去);
当AB=BP时,25+a2=62,解得:$a=\sqrt{11}$(负值已舍去);
当AP=BP时,1+a2=25+a2,不成立,
即当a 取$\sqrt{35}$或$\sqrt{11}$时,△ABP为等腰三角形;
③如图, 过点P作PH⊥x轴于H,
过点P作PH⊥x轴于H,
∵点A与点B,点P与点Q均关于M点成中心对称,
故四边形APBQ为平行四边形,
当∠APB=90°时,四边形APBQ为矩形,
此时△APH∽△PBH,
∴$\frac{AH}{HP}=\frac{HP}{BH}$,
即$\frac{1}{a}=\frac{a}{2m+3}$,
∴a2=2m+3,
∴$m=\frac{1}{2}{a^2}-\frac{3}{2}$,
当a=3时,$m=\frac{1}{2}×{3^2}-\frac{3}{2}=3$,
∴S=(2m+4)a=(2×3+4)×3=30.
点评 此题是二次函数综合题,主要考查了抛物线的顶点坐标的确定,旋转的性质,等腰三角形的性质,矩形的性质,相似三角形的判定和性质,解(2)①的关键是得出AM的长,解(2)②的关键是分类讨论,用等腰三角形的腰建立方程,解(2)③的关键是得出△APH∽△PBH,是一道中等难度的题目.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016~2017学年安徽省芜湖市九年级下学期第一次模拟考试数学试卷(解析版) 题型:填空题
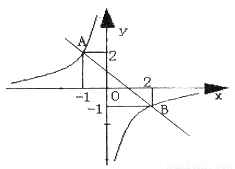
如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是 。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
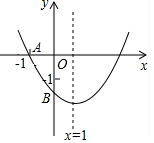 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac-b2<2a;④2b=3a.
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac-b2<2a;④2b=3a.| A. | ①③ | B. | ②④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
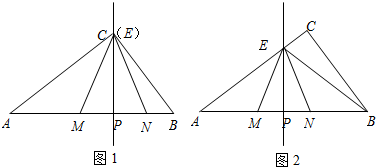
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com