
【题目】如图,梯形ABCD中,AD∥BC , ∠B=30°,∠C=60°,E、F、M、N分别为AB、CD、BC、DA的中点,若BC=7,MN=3,则EF为( ) 
A.3
B.4
C.5
D.6
【答案】B
【解析】解答:过点M分别作G∥AB , MH∥CD , 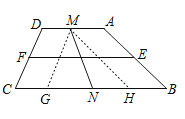
得平行四边形ABHM和平行四边形DCGM ,
∴∠NGM+∠NHM=∠B+∠C=90°,GH=BC-AD , MG=MH
∴GH=2MN=6(直角三角形斜边上的中线等于斜边的一半)
∴AD=7-6=1
∴EF=4,
故选B.
分析:过点N分别作NG∥AB , NH∥CD , 得平行四边形ABGN和平行四边形DCHN , 根据平行四边形的性质可得到△GNH为直角三角形,且MN为其斜边上的中线,由已知可求得AD的长,从而不难求中位线的长了 .
【考点精析】通过灵活运用梯形的中位线,掌握梯形的中位线平行于梯形的两底并等于两底和的一半即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,对角线AC、BD相交于点O , M、N分别是边AB、AD的中点,连接OM、ON、MN , 则下列叙述正确的是( ) 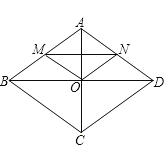
A.△AOM和△AON都是等边三角形
B.四边形MBON和四边形MODN都是菱形
C.四边形AMON和四边形ABCD都是位似图形
D.四边形MBCO和四边形NDCO都是等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠A=90°,角平分线AE、中线AD、高线AH的大小关系是( )
A.AH<AE<AD
B.AH<AD<AE
C.AH≤AD≤AE
D.AH≤AE≤AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC , AD平分∠BAC , DE∥AC交AB于E , 则S△EBD:S△ABC=( ) 
A.1:2
B.1:4
C.1:3
D.2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形OABC的顶点A,B的坐标分别为A(6,0),B(6,4),D是BC的中点,动点P从O点出发,以每秒1个单位长度的速度,沿着O→A→B→D运动,设点P运动的时间为t秒(0<t<13).
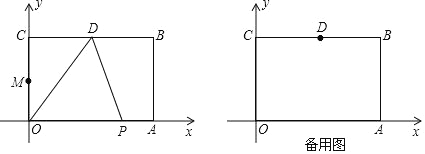
(1)①点D的坐标是(___,___);
②当点P在AB上运动时,点P的坐标是(___,___)(用t表示);
(2)写出△POD的面积S与t之间的函数关系式,并求出△POD的面积等于9时点P的坐标;
(3)当点P在OA上运动时,连接BP,将线段BP绕点P逆时针旋转,点B恰好落到OC的中点M处,则此时点P运动的时间t=___秒.(直接写出参考答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
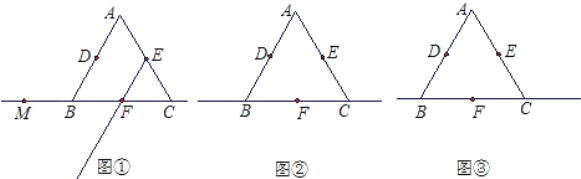
【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?画出图形,不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点. 
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S. 求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com