
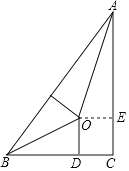
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的就用了这种分割方法,若BD=2,AE=3,则正方形ODCE的边长等于________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
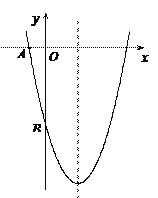
【题目】如图,已知二次函数![]() 的图象与坐标轴交于点A(-1, 0)和点B(0,-5).
的图象与坐标轴交于点A(-1, 0)和点B(0,-5).
(1)求该二次函数的解析式;
(2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为![]() ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.
①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校修建运动场,让甲工程队单独做需要15天完成,让乙工程队单独做需要10天完成.
(1)如果让甲、乙工程队合做3天后,剩下的工程由乙工程队完成,还需要多少天?
(2)已知甲队每天的费用为1000元,乙队每天的费用为1600 元,从节约资金的角度,认为是甲、乙队单独做,还是两队合做完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格线的交点叫格点,格点![]() 是
是![]() 的边
的边![]() 上的一点(请利用网格作图,保留作图痕迹).
上的一点(请利用网格作图,保留作图痕迹).

(1)过点![]() 画
画![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ;
;
(2)线段 的长度是点O到PC的距离;
(3)![]() 的理由是 ;
的理由是 ;
(4)过点C画![]() 的平行线;
的平行线;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学为推进书香校园建设,在全校范围开展图书漂流活动,现需要购进一批甲、乙两种规格的漂流书屋放置图书.已知一个甲种规格的漂流书屋的价格比一个乙种规格的漂流书屋的价格高80元;如果购买2个甲种规格的漂流书屋和3个乙种规格的漂流书屋,一共需要花费960元.
(1)求每个甲种规格的漂流书屋和每个乙种规格的漂流书屋的价格分别是多少元?
(2)如果学校计划购进这两种规格的漂流书屋共15个,并且购买这两种规格的漂流书屋的总费用不超过3040元,那么该学校至多能购买多少个甲种规格的漂流书屋?
查看答案和解析>>
科目:初中数学 来源: 题型:
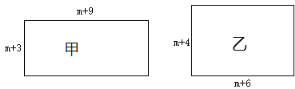
【题目】有甲、乙两个长方形纸片,边长如图所示![]() ,面积分别为
,面积分别为![]() 和
和![]() .
.
(1)①计算:![]() ______,
______,![]() ______;
______;
②用“<”“=”或“>”填空:![]() ______
______![]()
(2)若一个正方形纸片的周长与乙长方形的周长相等,面积为![]() .
.
①该正方形的边长是______(用含![]() 的代数式表示);
的代数式表示);
②小方同学发现:![]() 与
与![]() 的差与
的差与![]() 无关.请判断小方的发现是否正确,并通过计算说明你的理由.
无关.请判断小方的发现是否正确,并通过计算说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com