
分析 根据二次函数y=(k-1)x2+2kx-2=0的图象与x轴有两交点,可知(k-1)x2+2kx-2=0时,有两个不相等的实数根,从而可知△>0,又由y=(k-1)x2+2kx-2是二次函数得k-1≠0,从而可得k的取值范围.
解答 解:∵二次函数y=(k-1)x2+2kx-2的图象与x轴有两交点,
∴当y=0时,(k-1)x2+2kx-2=0有两个不相等的实数根.
∴△=b2-4ac=(2k)2-4(k-1)×(-2)>0.
解得k<-1-$\sqrt{3}$或k$>-1+\sqrt{3}$.
∵y=(k-1)x2+2kx-2是二次函数,
∴k-1≠0.
解得k≠1.
由上可得,k的取值范围是k<-1-$\sqrt{3}$或k$>-1+\sqrt{3}$且k≠1.
故答案为:k<-1-$\sqrt{3}$或k$>-1+\sqrt{3}$且k≠1.
点评 本题考查抛物线与x轴的交点、二次函数的定义,解题关键是能将二次函数与一元二次方程建立关系,根据根的情况,可知△的值.


科目:初中数学 来源: 题型:解答题
 如图,AC=BC,∠CAD=∠BCE,∠ACB=80°,∠E=100°.
如图,AC=BC,∠CAD=∠BCE,∠ACB=80°,∠E=100°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
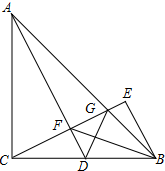 如图,△ABC中,AC=BC,∠ACB=90°,点D为BC的中点,点E与点C关于直线AD对称,CE与AD、AB分别交于点F、G,连接BE、BF、GD,求证:
如图,△ABC中,AC=BC,∠ACB=90°,点D为BC的中点,点E与点C关于直线AD对称,CE与AD、AB分别交于点F、G,连接BE、BF、GD,求证:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
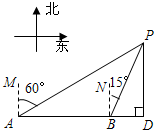 一艘轮船向正东航行,在A处测得灯塔P在A的北偏东60°方向,航行2小时到达B处,此时测得灯塔P在B的北偏东15°方向上,且灯塔P到轮船航线的距离PD是(10+10$\sqrt{3}$)海里,则轮船的航行速度为20海里/小时.
一艘轮船向正东航行,在A处测得灯塔P在A的北偏东60°方向,航行2小时到达B处,此时测得灯塔P在B的北偏东15°方向上,且灯塔P到轮船航线的距离PD是(10+10$\sqrt{3}$)海里,则轮船的航行速度为20海里/小时.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{80%}$元 | B. | 80%a元 | C. | 20%a元 | D. | $\frac{a}{20%}$元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com