
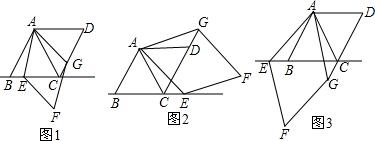
分析 (1)由菱形的性质可知:AE=AG,∠DAG=∠CAE.从而可证△ACE≌△ADG,利用全等三角形的性质即可得出AB、CG、CE之间的关系.
(2)同理可证△ACG≌△ABE(SAS),利用全等三角形的性质即可得出AB、CG、CE之间的关系.
解答 解:(1)AB=CG-CE
∵AC是菱形ABCD的对角线且∠BAC=60°,
∴AC=AD.
∵四边形AEFG菱形,
∴AE=AG.
∵∠DAC=∠GAE=60°,
∴∠DAG=∠CAE.
在△ACE与△ADG中,
$\left\{\begin{array}{l}{AE=AG}\\{∠CAE=∠DAG}\\{AC=AD}\end{array}\right.$
∴△ACE≌△ADG(SAS),
∴CE=DG..
∴AB=CD=CG-DG=CG-CE
(2)AB=CE-CG.
同理可证△ACG≌△ABE(SAS),
∴BE=CG.
∴AB=CB=CE-BE=CE-CG.
点评 本题考查全等三角形的判定与性质,涉及全等三角形的性质与判定方法,菱形的性质,等式的性质,本题属于中等题型.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=180}\\{0.9x+0.85y=250}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=180}\\{0.85x+0.9y=250}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=250}\\{0.9x+0.85y=180}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=180}\\{0.85x+0.9y=250}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
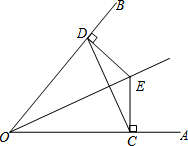 如图,点E是∠AOB平分线上的点,EC⊥OA于点C,ED⊥OB于点D,连接CD,求证:
如图,点E是∠AOB平分线上的点,EC⊥OA于点C,ED⊥OB于点D,连接CD,求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在学校的东边 | B. | 在东南方向800米处 | ||
| C. | 距学校800米处 | D. | 在学校东南方向800米处 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数是61 | B. | 中位数为57 | C. | 极差是39 | D. | 平均数为58 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).下列结论:
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛物线开口向上 | |
| B. | 顶点坐标为(-1,2) | |
| C. | 在对称轴的右侧,y随x的增大而增大 | |
| D. | 抛物线与x轴有两个交点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com