
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.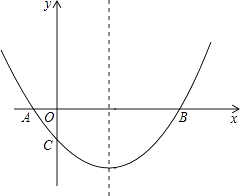
(1)求抛物线的解析式;
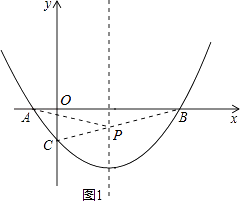
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
【答案】
(1)
解:设抛物线的解析式为y=ax2+bx+c(a≠0),
∵A(﹣1,0),B(5,0),C(0,- ![]() )三点在抛物线上,
)三点在抛物线上,
∴ 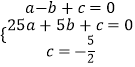 ,
,
解得 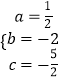 .
.
∴抛物线的解析式为:y= ![]() x2﹣2x﹣
x2﹣2x﹣ ![]()
(2)
解:∵抛物线的解析式为:y= ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() ,
,
∴其对称轴为直线x=﹣ ![]() =﹣
=﹣ ![]() =2,
=2,
连接BC,如图1所示,
∵B(5,0),C(0,﹣ ![]() ),
),
∴设直线BC的解析式为y=kx+b(k≠0),
∴ 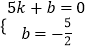 ,
,
解得 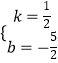 ,
,
∴直线BC的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
当x=2时,y=1﹣ ![]() =﹣
=﹣ ![]() ,
,
∴P(2,﹣ ![]() )
)
(3)
解:存在.
如图2所示,
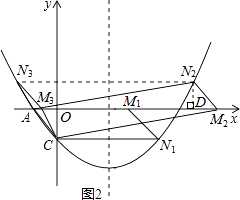
①当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C(0,﹣ ![]() ),
),
∴N1(4,﹣ ![]() );
);
②当点N在x轴上方时,
如图,过点N2作N2D⊥x轴于点D,
在△AN2D与△M2CO中,
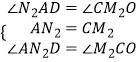
∴△AN2D≌△M2CO(ASA),
∴N2D=OC= ![]() ,即N2点的纵坐标为
,即N2点的纵坐标为 ![]() .
.
∴ ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() =
= ![]() ,
,
解得x=2+ ![]() 或x=2﹣
或x=2﹣ ![]() ,
,
∴N2(2+ ![]() ,
, ![]() ),N3(2﹣
),N3(2﹣ ![]() ,
, ![]() ).
).
综上所述,符合条件的点N的坐标为(4,﹣ ![]() ),(2+
),(2+ ![]() ,
, ![]() )或(2﹣
)或(2﹣ ![]() ,
, ![]() ).
).
【解析】(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(﹣1,0),B(5,0),C(0,- ![]() )三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
)三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.


科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,若“摸出的球是黑球”为必然事件,求m的值;
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于 ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中 ![]() 的长是cm(计算结果保留π).
的长是cm(计算结果保留π).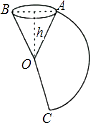
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD.连接PA,PB,PC,若PA=a,则点A到PB和PC的距离之和AE+AF= . 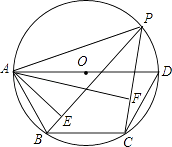
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=﹣ ![]() +x﹣4,下列说法正确的是( )
+x﹣4,下列说法正确的是( )
A.当x>0时,y随x的增大而增大
B.当x=2时,y有最大值﹣3
C.图象的顶点坐标为(﹣2,﹣7)
D.图象与x轴有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用的练习本,一般在甲、乙两家文具店购买,已知两家文具店的标价都是每本1元,但甲文具店的优惠条件是一次购买10本以上,从第11本起按标价的70%卖;乙文具店的优惠条件是全部按八五折优惠.
(1)若小明打算买30本,到哪家店购买省钱?
(2)小明现有38元钱,最多可买多少本练习本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com