
【题目】定义符号![]() 的含义为:当
的含义为:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 如:
如:![]() ,
,![]() =
=![]() 则
则![]() 的最大值是______.
的最大值是______.
【答案】![]()
【解析】
分析: 画出函数图象草图,利用函数图象的性质可得结论.
详解:在同一坐标系xOy中,画出函数二次函数y=-x2+1与正比例函数y=-x的图象,如图所示,
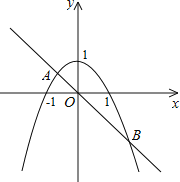
设它们交于点A、B,令-x2+1=-x,即x2-x-1=0,解得:x=![]() 或
或![]() ,
,
∴A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),观察图象可知:
),观察图象可知:
当x≤![]() 时,min{-x2+1,-x}=-x2+1,函数值随x的增大而增大,其最大值为
时,min{-x2+1,-x}=-x2+1,函数值随x的增大而增大,其最大值为![]() ,
,
当![]() <x≤
<x≤![]() 时,min{-x2+1,-x}=-x,函数值随x的增大而减小,没有最大值;
时,min{-x2+1,-x}=-x,函数值随x的增大而减小,没有最大值;
当x>![]() 时,min{-x2+1,-x}=-x2+1,函数值随x的增大而减小,最大值为
时,min{-x2+1,-x}=-x2+1,函数值随x的增大而减小,最大值为![]()
综上所示,min{-x2+1,-x}的最大值是![]() ,故答案为:
,故答案为:![]()
点睛: 本题考查了二次函数与正比例函数的图象与性质,充分理解定义min{a,b}和掌握函数的性质是解题的关键.


科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断

A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
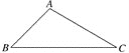
【题目】三角形中有3个角、3条边共6个元素,由其中的已知元素,求出所有未知元素的过程,叫做解三角形.
已知△ABC中,AB=![]() ,∠B=45°,BC=1+
,∠B=45°,BC=1+![]() ,解△ABC.
,解△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级根据学生的学习成绩、学习能力将学生依次分为A、B、C三个层次,第一次月考后,选取了其中一个A层次班级的考试成绩分布情况进行处理分析,制成频数分布表(成绩得分均为整数):
组别 | 成绩分组 | 频数 | 频率 |
1 | 39.5﹣49.5 | 2 | 0.05 |
2 | 49.5﹣59.5 | 4 | 0.10 |
3 | 59.5~69.5 | a | 0.20 |
4 | 69.5~79.5 | 10 | 0.25 |
5 | 79.5﹣89.5 | b | c |
6 | 89.5﹣100 | 6 | 0.15 |
合计 | 40 | 1.00 |
根据表中提供的信息解答下列各题:
(1)频数分布表中的a= ,b= ,c= ;
(2)将频数分布直方图补充完整;
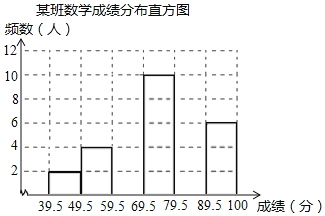
(3)小明正好在所选取的班级中,他认为:学校八年级共有20个班(平均每班40人),根据本班的成绩分布情况可知,在这次考试中,全年级90分以上为优秀,则优秀的人数约为 人,60分及以上为及格,及格的人数约为 人,及格的百分比约为 ;
(4)小明得到的数据会与实际情况相符吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,延长BA到点F,使得AF=AB,连接FC交AD于E.

(1)求证:AD与FC互相平分;
(2)当CF平分∠BCD时,BC与CD的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
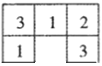
【题目】如图是一些由棱长均为![]() 的小立方块所搭的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.
的小立方块所搭的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.
(1)请分别画出这个几何体的主视图和左视图;
(2)求这个几何体的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
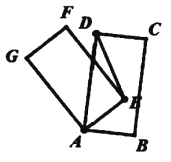
【题目】如图,将一个![]() 智屏手机抽象成一个的矩形
智屏手机抽象成一个的矩形![]() ,其中
,其中![]() ,
,![]() ,然后将它围绕顶点
,然后将它围绕顶点![]() 逆时针旋转一周,旋转过程中
逆时针旋转一周,旋转过程中![]() 、
、![]() 、
、![]() 、
、![]() 的对应点依次为
的对应点依次为![]() 、
、![]() 、
、![]() 、
、![]() ,则当
,则当![]() 为直角三角形时,若旋转角为
为直角三角形时,若旋转角为![]() ,则
,则![]() 的大小为______.
的大小为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳池普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元张,每次凭卡不再收费;
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常销售,两种优惠卡仅限暑假使用,每人一次一张票不限次数.
(1)分别写出选择普通票、银卡消费时,所需费用![]() 、
、![]() 与次数
与次数![]() 之间的函数表达式;
之间的函数表达式;
(2)小明打算暑假每天游泳一次,按55天计算,则选择哪种消费方式更合算?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com