
”¾ĢāÄæ”æŅŃÖŖÖ±Ļßl1”Īl2 £¬ µćAŹĒl1ÉĻµÄ¶Æµć£¬µćBŌŚl1ÉĻ£¬µćC”¢DŌŚl2ÉĻ£¬”ĻABC£¬”ĻADCµÄĘ½·ÖĻß½»ÓŚµćE£Ø²»ÓėµćB£¬DÖŲŗĻ£©£®
£Ø1£©ČōµćAŌŚµćBµÄ×ó²ą£¬”ĻABC=80”ć£¬”ĻADC=60”ć£¬¹żµćE×÷EF”Īl1 £¬ ČēĶ¼¢ŁĖłŹ¾£¬Ēó”ĻBEDµÄ¶ČŹż£® 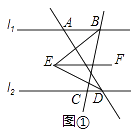
£Ø2£©ČōµćAŌŚµćBµÄ×ó²ą£¬”ĻABC=¦Į”ć£¬”ĻADC=60”ć£¬ČēĶ¼¢ŚĖłŹ¾£¬Ēó”ĻBEDµÄ¶ČŹż£»£ØÖ±½ÓŠ“³ö¼ĘĖćµÄ½į¹ū£© 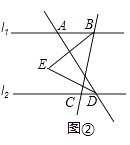
£Ø3£©ČōµćAŌŚµćBµÄÓŅ²ą£¬”ĻABC=¦Į”ć£¬”ĻADC=60”ć£¬ČēĶ¼¢ŪĖłŹ¾£¬Ēó”ĻBEDµÄ¶ČŹż£® 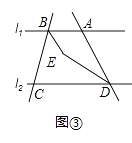
”¾“š°ø”æ
£Ø1£©½ā£ŗ”ßBE”¢DE·Ö±šŹĒ”ĻABC£¬”ĻADCµÄĘ½·ÖĻߣ¬
”ą”ĻABE= ![]() ”ĻABC=
”ĻABC= ![]() ”Į80”ć=40”ć£¬”ĻCDE=
”Į80”ć=40”ć£¬”ĻCDE= ![]() ”ĻADC=
”ĻADC= ![]() ”Į60”ć=30”ć£®
”Į60”ć=30”ć£®
”ßEF”ĪL1£¬
”ą”ĻBEF=”ĻABE=40”ć£®
”ßL1”ĪL2
”ąEF”ĪL2
”ą”ĻDEF=”ĻCDE=30”ć
”ą”ĻBED=”ĻBEF+”ĻDEF=40”ć+30”ć=70”ć
£Ø2£©½ā£ŗBE”¢DE·Ö±šŹĒ”ĻABC£¬”ĻADCµÄĘ½·ÖĻߣ¬
”ą”ĻABE= ![]() ”ĻABC=
”ĻABC= ![]() ¦Į”ć£¬”ĻCDE=
¦Į”ć£¬”ĻCDE= ![]() ”ĻADC=
”ĻADC= ![]() ”Į60”ć=30”ć£®
”Į60”ć=30”ć£®
”ßEF”ĪL1£¬
”ą”ĻBEF=”ĻABE= ![]() ¦Į”ć£®
¦Į”ć£®
”ßL1”ĪL2£¬
”ąEF”ĪL2£¬
”ą”ĻDEF=”ĻCDE=30”ć
”ą”ĻBED=”ĻBEF+”ĻDEF= ![]() ¦Į”ć+30”ć£¬¼“”ĻBED=£Ø
¦Į”ć+30”ć£¬¼“”ĻBED=£Ø ![]() ¦Į+30£©”ć
¦Į+30£©”ć
£Ø3£©½ā£ŗ¹żµćE×÷EF”ĪL1£¬
”ßBE£¬DE·Ö±šŹĒ”ĻABC”¢”ĻADCĘ½·ÖĻߣ¬
”ą”ĻABE= ![]() ”ĻABC=
”ĻABC= ![]() ¦Į”ć£¬”ĻCDE=
¦Į”ć£¬”ĻCDE= ![]() ”ĻADC=
”ĻADC= ![]() ”Į60”ć=30”ć£®
”Į60”ć=30”ć£®
”ßEF”ĪL1£¬
”ą”ĻBEF=£Ø180© ![]() ¦Į£©”ć£®
¦Į£©”ć£®
ÓÖ”ßL1”ĪL2
”ąEF”ĪL2
”ą”ĻDEF=”ĻCDE=30”ć
”ą”ĻBED=”ĻBEF+”ĻDEF
=£Ø180© ![]() ¦Į+30£©”ć
¦Į+30£©”ć
=£Ø210© ![]() ¦Į£©”ć
¦Į£©”ć
”¾½āĪö”æ£Ø1£©øł¾ŻBE”¢DE·Ö±šŹĒ”ĻABC£¬”ĻADCµÄĘ½·ÖĻߣ¬µĆ³ö”ĻABE= ![]() ”ĻABC£¬”ĻCDE=
”ĻABC£¬”ĻCDE= ![]() ”ĻADC£¬ŌŁÓÉĘ½ŠŠĻߵĊŌÖŹµĆ³ö”ĻBEF=”ĻABE£¬Ķ¬ĄķæÉµĆ³ö”ĻDEF=”ĻCDE£¬ŌŁÓÉ”ĻBED=”ĻBEF+”ĻDEF¼“æÉµĆ³ö½įĀŪ£»£Ø2£©¹żµćE×÷EF”ĪAB£¬Ķ¬£Ø1£©µÄÖ¤Ć÷¹ż³ĢĶźČ«ĻąĶ¬£»£Ø3£©¹żµćE×÷EF”ĪL1 £¬ øł¾ŻBE£¬DE·Ö±šŹĒ”ĻABC”¢”ĻADCĘ½·ÖĻßæÉÖŖ”ĻABE=
”ĻADC£¬ŌŁÓÉĘ½ŠŠĻߵĊŌÖŹµĆ³ö”ĻBEF=”ĻABE£¬Ķ¬ĄķæÉµĆ³ö”ĻDEF=”ĻCDE£¬ŌŁÓÉ”ĻBED=”ĻBEF+”ĻDEF¼“æÉµĆ³ö½įĀŪ£»£Ø2£©¹żµćE×÷EF”ĪAB£¬Ķ¬£Ø1£©µÄÖ¤Ć÷¹ż³ĢĶźČ«ĻąĶ¬£»£Ø3£©¹żµćE×÷EF”ĪL1 £¬ øł¾ŻBE£¬DE·Ö±šŹĒ”ĻABC”¢”ĻADCĘ½·ÖĻßæÉÖŖ”ĻABE= ![]() ”ĻABC=
”ĻABC= ![]() ¦Į”ć£¬”ĻCDE=
¦Į”ć£¬”ĻCDE= ![]() ”ĻADC£¬ŌŁÓÉEF”ĪL1æÉÖŖ”ĻBEF=£Ø180©
”ĻADC£¬ŌŁÓÉEF”ĪL1æÉÖŖ”ĻBEF=£Ø180© ![]() ¦Į£©”ć£®øł¾ŻL1”ĪL2æÉÖŖEF”ĪL2 £¬ ¹Ź”ĻDEF=”ĻCDE=30”ć£¬ĖłŅŌ”ĻBED=”ĻBEF+”ĻDEF£®
¦Į£©”ć£®øł¾ŻL1”ĪL2æÉÖŖEF”ĪL2 £¬ ¹Ź”ĻDEF=”ĻCDE=30”ć£¬ĖłŅŌ”ĻBED=”ĻBEF+”ĻDEF£®
”¾æ¼µć¾«Īö”æ±¾ĢāÖ÷ŅŖæ¼²éĮĖĘ½ŠŠĻߵĊŌÖŹµÄĻą¹ŲÖŖŹ¶µć£¬ŠčŅŖÕĘĪÕĮ½Ö±ĻßĘ½ŠŠ£¬Ķ¬Ī»½ĒĻąµČ£»Į½Ö±ĻßĘ½ŠŠ£¬ÄŚ“ķ½ĒĻąµČ£»Į½Ö±ĻßĘ½ŠŠ£¬Ķ¬ÅŌÄŚ½Ē»„²¹²ÅÄÜÕżČ·½ā“š“ĖĢā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
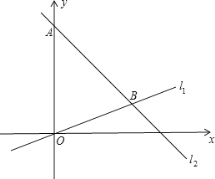
”¾ĢāÄæ”æŅŃÖŖ£¬ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÄŚ£¬µćAµÄ×ų±źĪŖ£Ø0£¬24 £©£¬¾¹żŌµćµÄÖ±Ļßl1Óė¾¹żµćAµÄÖ±Ļßl2Ļą½»ÓŚµćB£¬µćB×ų±źĪŖ£Ø18£¬6£©.
(1)ĒóÖ±Ļßl1£¬l2µÄ±ķ“ļŹ½£»
(2)µćCĪŖĻ߶ĪOBÉĻŅ»¶Æµć £ØµćC²»ÓėµćO£¬BÖŲŗĻ£©£¬×÷CD”ĪyÖį½»Ö±Ļßl2ÓŚµćD£¬¹żµćC£¬D·Ö±šĻņyÖį×÷“¹Ļߣ¬“¹×ć·Ö±šĪŖF£¬E£¬µĆµ½¾ŲŠĪCDEF.
¢ŁÉčµćCµÄׯ×ų±źĪŖa£¬ĒóµćDµÄ×ų±ź£ØÓĆŗ¬aµÄ“śŹżŹ½±ķŹ¾£©£»
¢ŚČō¾ŲŠĪCDEFµÄĆ껿ĪŖ60£¬ĒėÖ±½ÓŠ“³ö“ĖŹ±µćCµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬µćAµÄ×ų±źĪŖ(2£¬1)£¬Õż±ČĄżŗÆŹży=kxµÄĶ¼ĻóÓėĻ߶ĪOAµÄ¼Š½ĒŹĒ45”ć£¬ĒóÕāøöÕż±ČĄżŗÆŹżµÄ±ķ“ļŹ½ĪŖ___________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ°Ń¶ąĻīŹ½x3-2x2+x·Ö½āŅņŹ½½į¹ūÕżČ·µÄŹĒ£Ø””£©
A. x£Øx2-2x£© B. x2£Øx-2£© C. x£Øx+1£©£Øx-1£© D. x£Øx-1£©2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōŅ»×鏿¾Ż4£¬1£¬6£¬x£¬5µÄĘ½¾łŹżĪŖ4£¬ŌņÕā×鏿¾ŻµÄÖŚŹżĪŖ£Ø””””£©
A. 6B. 5C. 4D. 3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼Ö±½Ē×ų±źĻµÖŠ£¬¾ŲŠĪABCDµÄ±ßBCŌŚxÖįÉĻ£¬µćB”¢DµÄ×ų±ź·Ö±šĪŖB£Ø1£¬0£©£¬D£Ø3£¬3£©£®
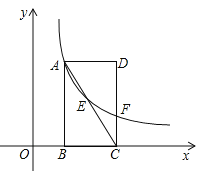
£Ø1£©µćCµÄ×ų±ź £»
£Ø2£©Čō·“±ČĄżŗÆŹż![]() µÄĶ¼Ļó¾¹żÖ±ĻßACÉĻµÄµćE£¬ĒŅµćEµÄ×ų±źĪŖ£Ø2£¬m£©£¬ĒómµÄÖµ¼°·“±ČĄżŗÆŹżµÄ½āĪöŹ½£»
µÄĶ¼Ļó¾¹żÖ±ĻßACÉĻµÄµćE£¬ĒŅµćEµÄ×ų±źĪŖ£Ø2£¬m£©£¬ĒómµÄÖµ¼°·“±ČĄżŗÆŹżµÄ½āĪöŹ½£»
£Ø3£©Čō£Ø2£©ÖŠµÄ·“±ČĄżŗÆŹżµÄĶ¼ĻóÓėCDĻą½»ÓŚµćF£¬Į¬½ÓEF£¬ŌŚÖ±ĻßABÉĻÕŅŅ»µćP£¬Ź¹µĆ![]() £¬ĒóµćPµÄ×ų±ź£®
£¬ĒóµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ£ŗEŹĒ”ĻAOBµÄĘ½·ÖĻßÉĻŅ»µć£¬EC”ĶOB£¬ED”ĶOA£¬C”¢DŹĒ“¹×ć£¬Į¬½ÓCD£¬ĒŅ½»OEÓŚµćF.
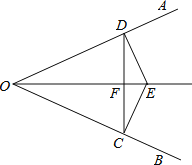
(1)ĒóÖ¤£ŗOEŹĒCDµÄ“¹Ö±Ę½·ÖĻß.
(2)Čō”ĻAOB=60”ć£¬ĒėÄćĢ½¾æOE£¬EFÖ®¼äÓŠŹ²Ć“ŹżĮæ¹ŲĻµ?²¢Ö¤Ć÷ÄćµÄ½įĀŪ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ā¾öĻĀĮŠø÷Š”Ģā£ØµŚ¢ŁĢā4·Ö£¬Ćæ¢ŚĢā5·Ö£¬µŚ¢ŪĢā6·Ö£¬Āś·Ö15·Ö£©
¢ŁŅņŹ½·Ö½ā£ŗ ![]() £®
£®
¢Ś½ā²»µČŹ½×é£ŗ 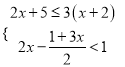 £¬²¢Öø³öĖüµÄĖłÓŠ·ĒøŗÕūŹż½ā£®
£¬²¢Öø³öĖüµÄĖłÓŠ·ĒøŗÕūŹż½ā£®
¢Ū»Æ¼ņ£ŗ ![]() £¬ŌŁ“Ó
£¬ŌŁ“Ó![]() £¬
£¬ ![]() £¬
£¬ ![]() £¬
£¬ ![]() ÖŠŃ”Ņ»øöŗĻŹŹµÄŹż“śČėĒóÖµ£®
ÖŠŃ”Ņ»øöŗĻŹŹµÄŹż“śČėĒóÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com