
【题目】如图所示,已知A,B两点的坐标分别为(2![]() ,0),(0,10),P是△AOB外接圆⊙C上的一点,OP交AB于点 D.
,0),(0,10),P是△AOB外接圆⊙C上的一点,OP交AB于点 D.
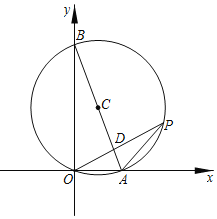
(1)当OP⊥AB时,求OP;
(2)当∠AOP=30°时,求AP.
科目:初中数学 来源: 题型:
【题目】某校举行了自贡市创建全国文明城市知识竞赛活动,初一年级全体同学参加了知识竞赛.
收集教据:现随机抽取了初一年级![]() 名同学的“创文知识竞赛”成绩,分数如下(单位:分):
名同学的“创文知识竞赛”成绩,分数如下(单位:分):
整理分析数据:
成绩 | 频数(人数) |
|
|
|
|
|
|
|
|
(1)请将图表中空缺的部分补充完整;
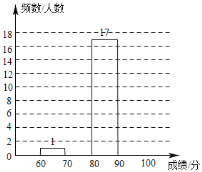
(2)学校决定表彰“创文知识竞赛”成绩在![]() 分及其以上的同学.根据上面统计结果估计该校初一年级
分及其以上的同学.根据上面统计结果估计该校初一年级![]() 人中,约有多少人将获得表彰;
人中,约有多少人将获得表彰;
(3)“创文知识竞赛”中,受到表彰的小红同学得到了印有龚扇、剪纸、彩灯、恐龙图案的四枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有恐龙图案的概率是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,AB=![]() ,点E,F同时从B点出发,沿射线BC向右匀速移动,已知点F的移动速度是点E移动速度的2倍,以EF为一边在CB的上方作等边△EFG,设E点移动距离为x(0<x<6).
,点E,F同时从B点出发,沿射线BC向右匀速移动,已知点F的移动速度是点E移动速度的2倍,以EF为一边在CB的上方作等边△EFG,设E点移动距离为x(0<x<6).
(1)∠DCB= 度,当点G在四边形ABCD的边上时,x= ;
(2)在点E,F的移动过程中,点G始终在BD或BD的延长线上运动,求点G在线段BD的中点时x的值;
(3)当2<x<6时,求△EFG与四边形ABCD重叠部分面积y与x之间的函数关系式,当x取何值时,y有最大值?并求出y的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c的图象与x轴交于A(﹣3,0)、B(2,0)两点,与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)点E(m,2)是直线AC上方的抛物线上一点,连接EA、EB、EC,EB与y轴交于D.
①点F是x轴上一动点,连接EF,当以A、E、F为顶点的三角形与△BOD相似时,求出线段EF的长;
②点G为y轴左侧抛物线上一点,过点G作直线CE的垂线,垂足为H,若∠GCH=∠EBA,请直接写出点H的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
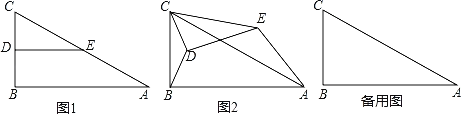
【题目】如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,![]() =_______;
=_______;
②当α=180°时,![]() =______.
=______.
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
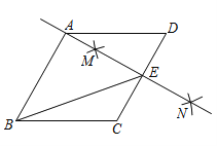
【题目】如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于![]() 为半径作弧,两弧交于点M,N;②作直线MN,且
为半径作弧,两弧交于点M,N;②作直线MN,且![]() 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
A.![]() B.
B.![]() C.若AB=4,则
C.若AB=4,则![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了做好开学准备,某校共购买了20桶A、B两种桶装消毒液,进行校园消杀,以备开学.已知A种消毒液300元/桶,每桶可供2 000米2的面积进行消杀,B种消毒液200元/桶,每桶可供1 000米2的面积进行消杀.
(1)设购买了A种消毒液x桶,购买消毒液的费用为y元,写出y与x之间的关系式,并指出自变量x的取值范围;
(2)在现有资金不超过5 300元的情况下,求可消杀的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O的半径为r,在射线OM上任取一点P(不与点O重合),如果射线OM上的点P',满足OP·OP'=r2,则称点P'为点P关于⊙O的反演点.

在平面直角坐标系xOy中,已知⊙O的半径为2.
(1)已知点A (4,0),求点A关于⊙O的反演点A'的坐标;
(2)若点B关于⊙O的反演点B'恰好为直线![]() 与直线x=4的交点,求点B的坐标;
与直线x=4的交点,求点B的坐标;
(3)若点C为直线![]() 上一动点,且点C关于⊙O的反演点C'在⊙O的内部,求点C的横坐标m的范围;
上一动点,且点C关于⊙O的反演点C'在⊙O的内部,求点C的横坐标m的范围;
(4)若点D为直线x=4上一动点,直接写出点D关于⊙O的反演点D'的横坐标t的范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com