
 -$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$=$\frac{x+1}{x-1}$
-$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$=$\frac{x+1}{x-1}$分析 (1)设所捂部分为A,根据题意得出A的表达式,再根据分式混合运算的法则进行计算即可;
(2)令原代数式的值为-1,求出x的值,代入代数式中的式子进行验证即可.
解答 解:(1)设所捂部分为A,
则A=$\frac{x+1}{x-1}$•$\frac{x}{x+1}$+$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$
=$\frac{x}{x-1}$+$\frac{x+1}{x-1}$
=$\frac{x+x+1}{x-1}$
=$\frac{2x+1}{x-1}$;
(2)若原代数式的值为-1,则$\frac{x+1}{x-1}$=-1,即x+1=-x+1,解得x=0,
当x=0时,除式$\frac{x}{x+1}$=0,
故原代数式的值不能等于-1.
点评 本题考查的是分式的化简求值,在解答此类提问题时要注意x的取值要保证每一个分式有意义.


科目:初中数学 来源: 题型:解答题
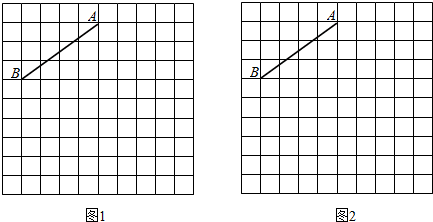
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
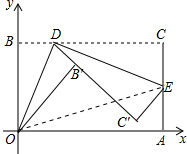 如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.
如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
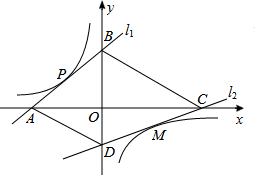 如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(-1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )
如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(-1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )| A. | (1,-1) | B. | (2,-$\frac{1}{2}$) | C. | (3,-$\frac{1}{3}$) | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com